Цель:
Определение напряженно деформированного состояния цилиндра со свободными торцами под внутренним давлением.
Литература:
Warren C. Young, Richard G. Budynas. Roark’s Formulas for Stress and Strain. Seventh Edition. New York, McGraw-Hill, 2002.
Формулировка задачи:
Определить напряжение в стенке цилиндра в меридиальном σ1 и окружном σ2 направлениях, а также меридиальные Δу и радиальные перемещения ΔR.
Описание расчетной схемы:
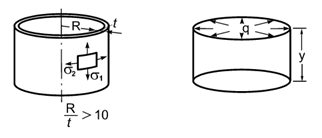
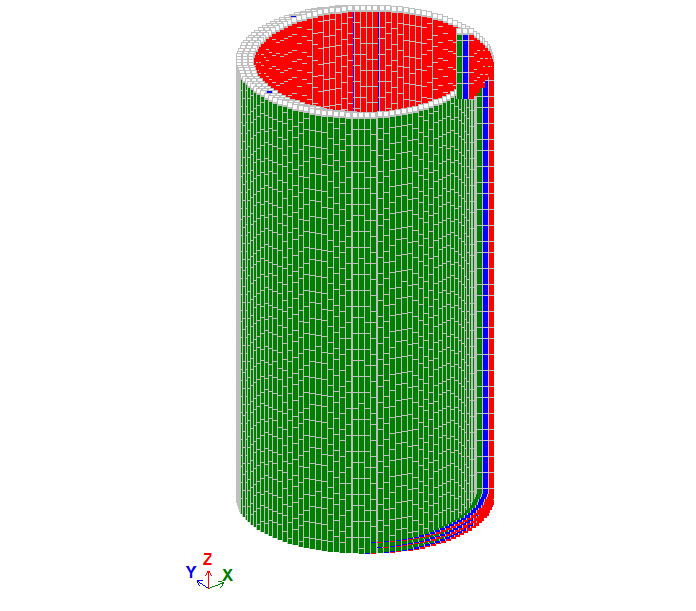
Цилиндр свободен от закреплений под воздействием внутреннего равномерного давления q.
|
Вариант 1 |
Вариант 2 |
Геометрия:
Радиус цилиндра R = 1 м;
Толщина стенки цилиндра t = 0,02 м;
Высота цилиндра L = 4 м.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Коэффициент Пуассона ν = 0,3.
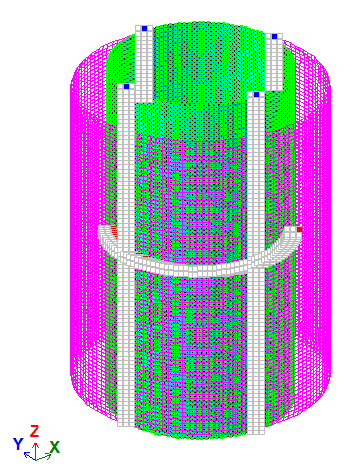
Граничні умови:
Связи симметрии.
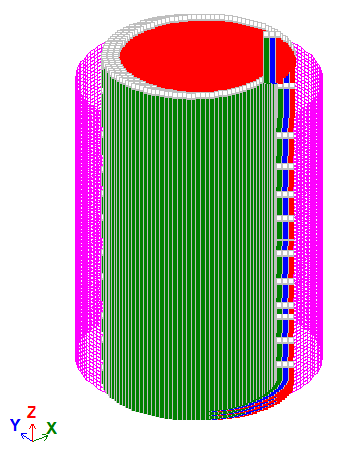
Нагрузки:
Внутреннее давление p = 10000 Па
Примечание:
Задача решается в пространственной постановке (признак схемы 5).
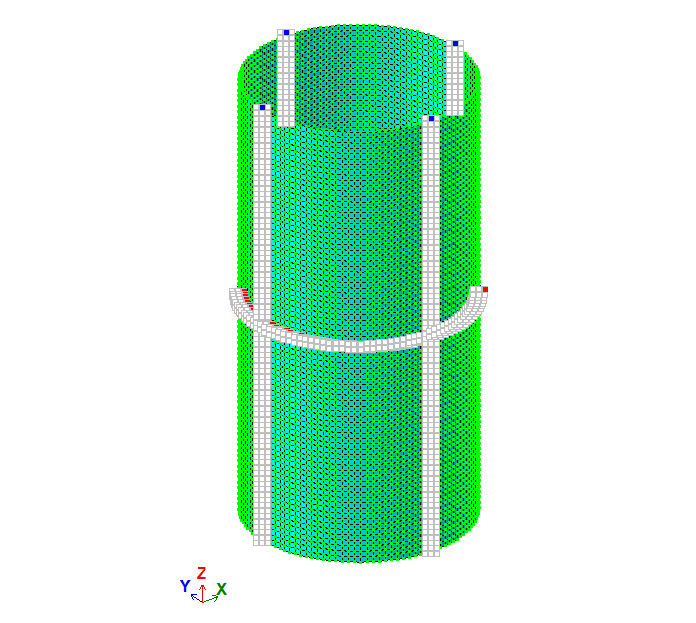
Для построения схемы использованы КЭ 44 – универсальный четырехугольный КЭ оболочки.
При решении задачи были рассмотрены два варианта:
мембранная теория оболочек (вариант 1) и общая теория оболочек (вариант 2).
Работа цилиндрической оболочки в соответствии с мембранной теорией достигается путем наложения связей на все угловые перемещения во всех узлах расчетной схемы.
Узлам схемы назначена местная система координат (местные оси узлов Х1 направлены от центра цилиндра).
Сетка конечных элементов имеет 80 элементов по высоте цилиндра и 120 элементов вдоль окружности.
Размер конечных элементов: 0,05 х 0,0525 м.
Количество узлов: 9720. Количество элементов: 9600.
Результаты расчета:
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
Аналитическое решение:
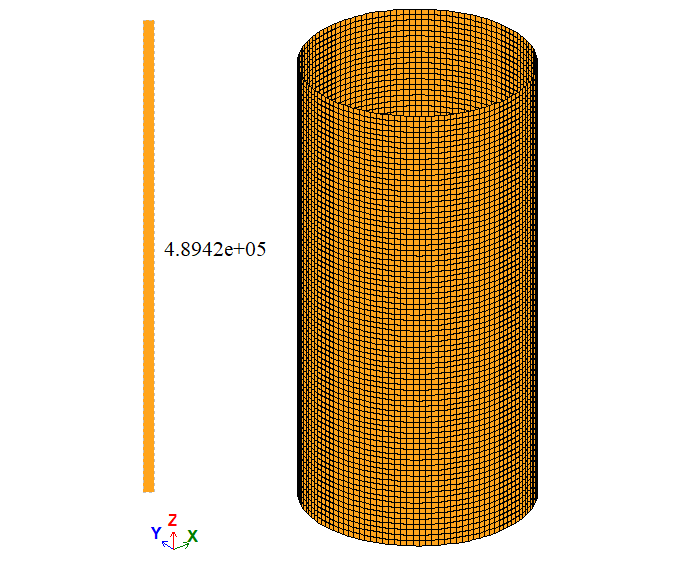
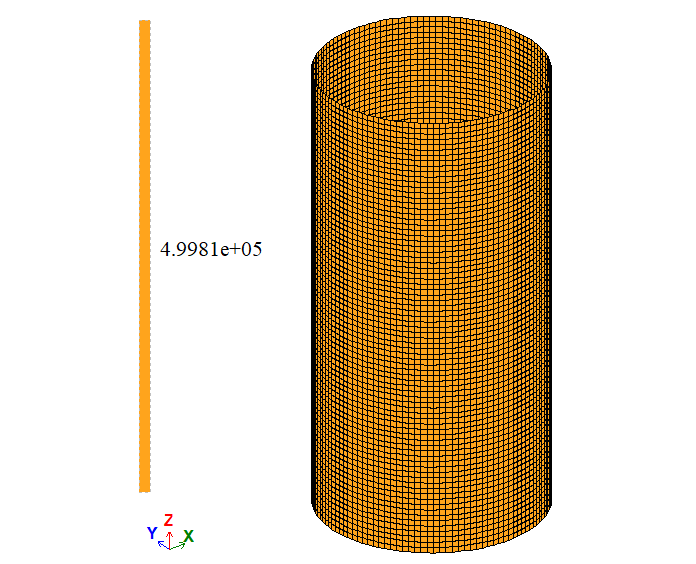
σ1 = p/t
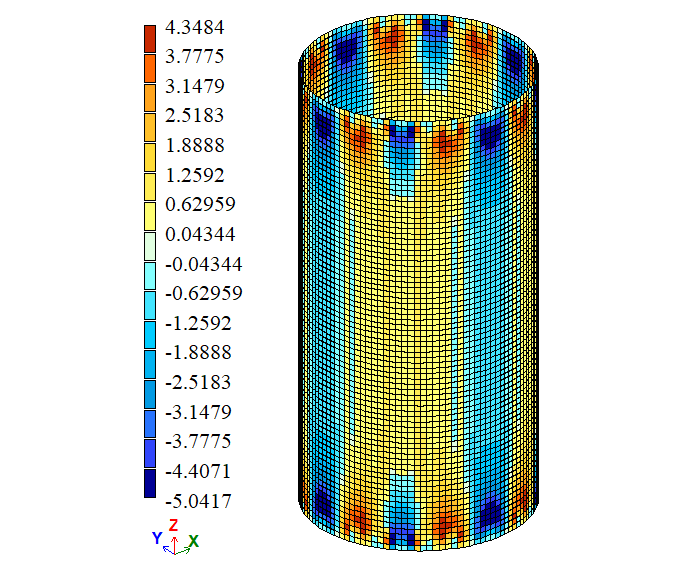
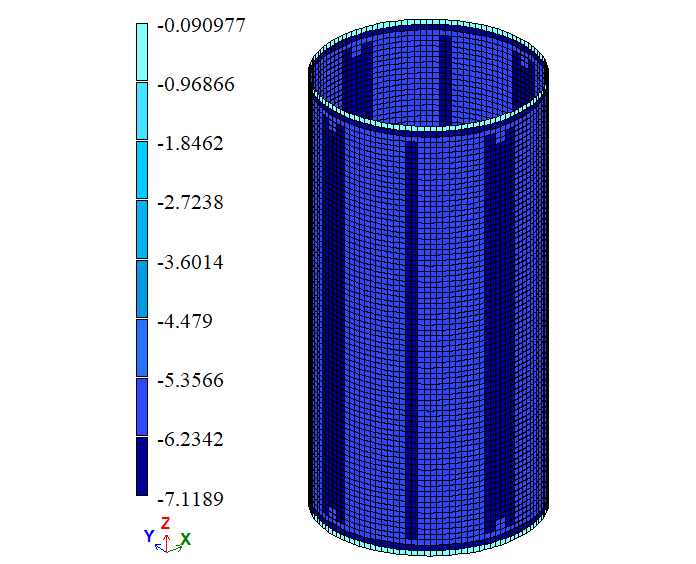
σ2 = 0
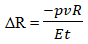
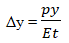
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | ||
| Вариант 1 | Вариант 2 | Вариант 1 | Вариант 2 | |||
| Точка на поверхности | σ1, Па | 5 * 105 | 4,8942*105 | 4,9981*105 | 2,116 | 0,038 |
| σ2, Па | 0 |
-5,0417 4,3484 |
-7,1189 -0,09097 |
- | - | |
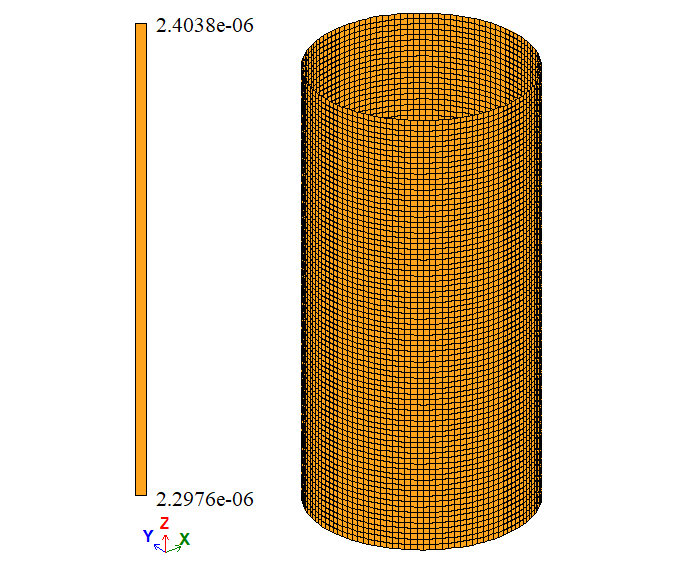
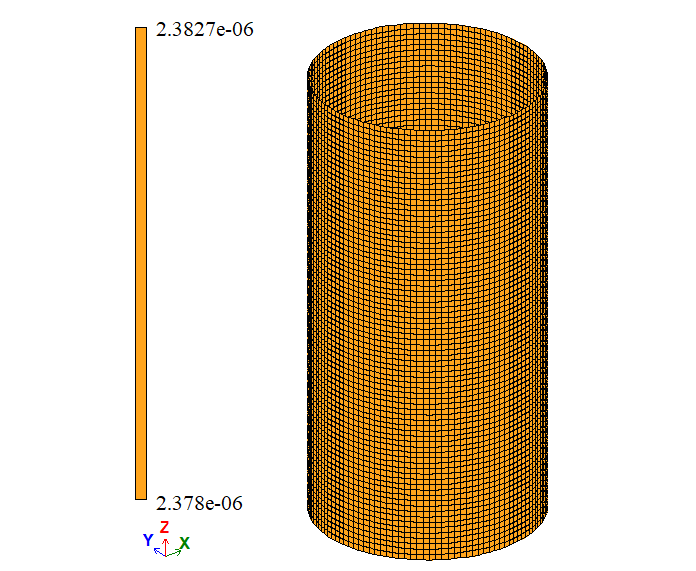
| ΔR, м | 2,38 * 10-6 | 2,3798*10-6 | 2,3803*10-6 | 0,0084 | 0,0126 | |
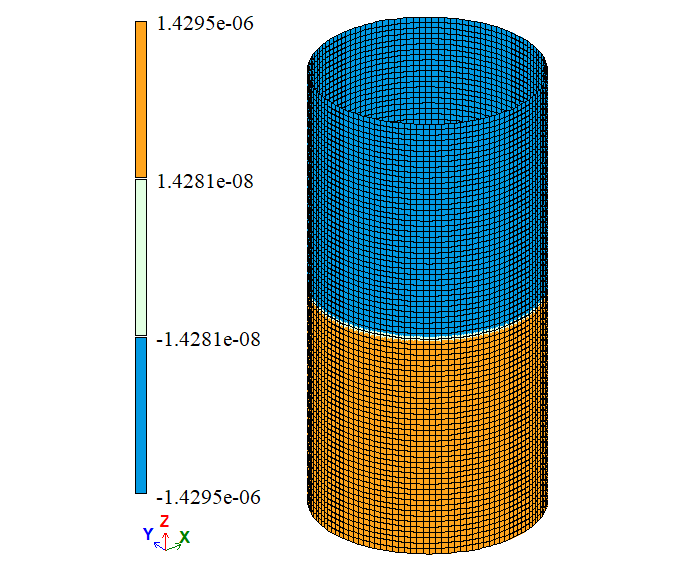
| Δy, м | -2,86 * 10-6 | -2,859 * 10-6 | -2,859 * 10-6 | 0,038 | 0,035 | |
|
Примечание: Поскольку при задании граничных условий применялись связи симметрии (закрепление по Z в середине высоты цилиндра), то величина вертикального перемещения в таблице увеличена в 2 раза. |
||||||
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Комментарии