Цель:
Определение напряженно-деформированного состояния системы перекрестных стержней от воздействия распределенной нагрузки и сосредоточенной силы в их плоскости.
Литература:
S. Timoshenko et D.H. Young, Theorie des constructions, Paris, Librairie Polytechnique Beranger, 1949, p. 412-416.
Формулировка задачи:
Определить в общем узле перекрестных стержней (точка А) угол поворота UY и изгибающие моменты M в стержнях с обеих сторон от узла.
Описание расчетной схемы:
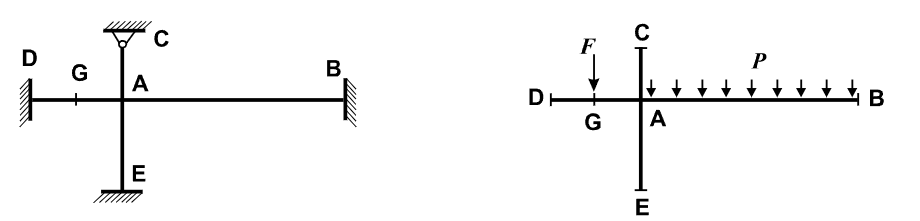
Система состоит из двух перекрестных стержней квадратного поперечного сечения, горизонтального (BD) и вертикального (КЭ), жестко соединенных в общем узле (точка А).
Горизонтальный стержень жестко защемлен в левом и правом узлах (точки D и B).
Вертикальный стержень жестко защемлен в нижнем узле (точка E) и шарнирно оперт в верхнем узле (точка C).
В середине левого пролета горизонтального стержня (точка G) приложена вертикальная сосредоточенная сила F на правом пролете горизонтального стержня (AB) расположена вертикальная равномерно распределенная нагрузка p.
|
|
|
|
Начальная геометрия аналитической схемы
|
Начальная геометрия КЭ модели
|
Геометрия:
Длина левого пролета горизонтального стержня: LАD = 1,0 м;
Сторона поперечного сечения левого пролета горизонтального стeржня: bAD = 1,0 м;
Длина правого пролета горизонтального стержня: LАB = 4,0 м;
Сторона поперечного сечения правого пролета горизонтального стeржня: bAB = 4,0 м;
Длина верхнего участка вертикального стержня LАС = 1,0 м;
Сторона поперечного сечения верхнего участка вертикального стeржня: bAС = 1,0 м;
Длина нижнего участка вертикального стержня LАЕ = 2,0 м;
Сторона поперечного сечения нижнего участка вертикального стeржня: bAЕ = 2,0 м
Характеристика материала:
Модуль упругости стержней системы Е = 2,0 * 1011 Па
Нагрузки:
Вертикальная сосредоточенная сила: F = 100 кН;
Значение вертикальной равномерно распределенной нагрузки: p = 1,0 кН/м
Примечание:
Расчетная схема — плоская рама, 5 стержневых элементов типа 10.
Обеспечение граничных условий достигается за счет наложения связей: по направлениям степеней свободы X, Z для шарнирно опертого узла (точка C) и по направлениям степеней свободы X, Z, UY для жестко защемленных узлов.
Количество узлов в расчетной схеме — 6.
Результаты расчета:
|
|
|
|
|
Расчетная и деформированная схема фермы
|
Значение углов поворота UY (рад*1000)
|
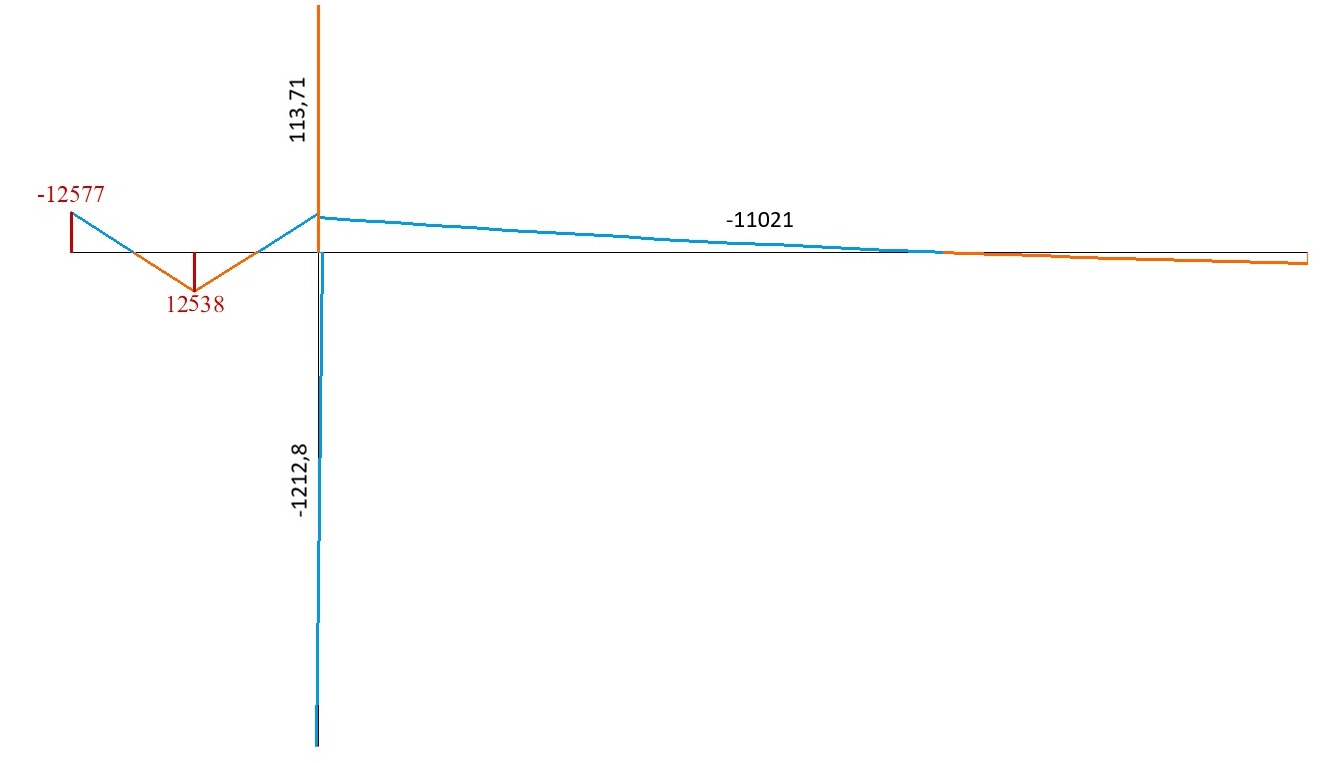
Значение изгибающих моментов M (Н * м)
|
Сравнение результатов расчета:
| Параметры | Аналитическое решение | LIRA-FEM | Погрешность, % |
| Угол поворота UY (точка A), рад*1000 | -227,12 | -227,4 | 0,12 |
| Изгибающий момент M (стержень AD), Н * м | -12348,6 | -12348 | 0,01 |
| Изгибающий момент M (стержень AВ), Н * м | -11023,7 | -11021 | 0,02 |
| Изгибающий момент M (стержень AС), Н * м | 113,6 | 113,71 | 0,09 |
| Изгибающий момент M (стержень AЕ), Н * м | -1211,3 | -1212,8 | 0,12 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Комментарии