Тест 1.27. Защемленная по концам балка, нагруженная равномерно-распределенной нагрузкой

Цель:

Нагрузка балки, защемленной по концам, в одной плоскости без учета деформаций поперечного сдвига. Проверяются значения максимального поперечного перемещения и изгибающих моментов.

Литература:

Писаренко Г.С., Яковлєв А.П., Матвєєв В.В. Довідник з опору матеріалів. — Київ: Наук. думка, 1988.

Формулировка задачи:

Определить максимальные поперечные перемещения w и изгибающие моменты M.

Описание расчетной схемы:

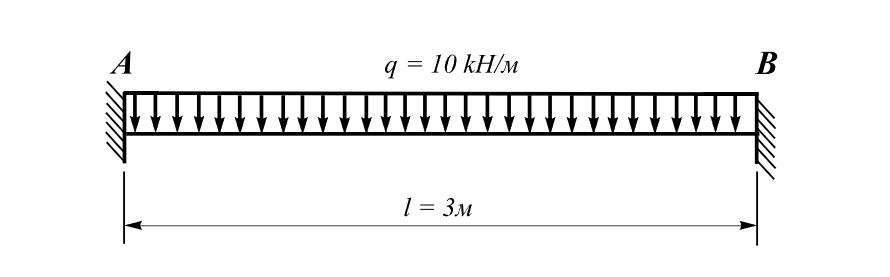
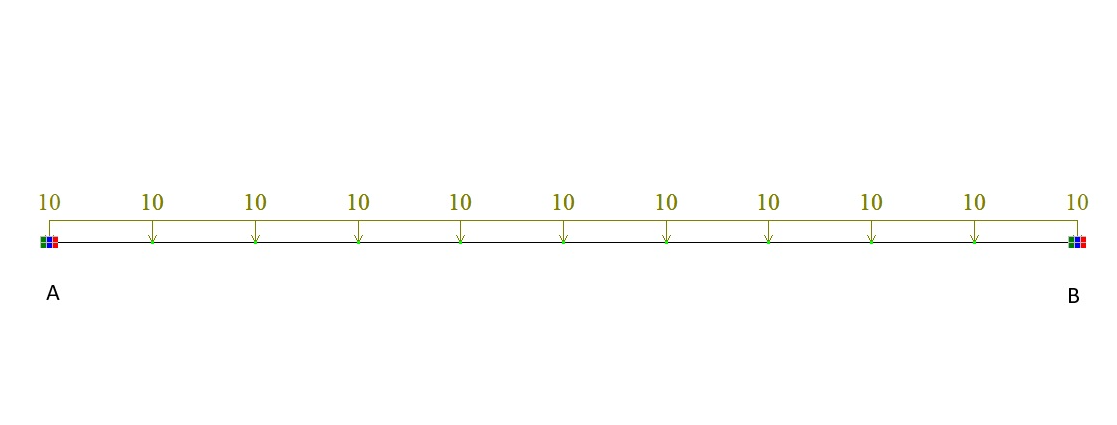
Балка, зажатая по концам, нагружается равномерно распределенной нагрузкой q.

Геометрия:

Длина балки L = 3 м;
Момент инерции I = 2,44 * 10^-6 м⁴;
Площадь поперечного сечения F = 14,2 * 10^-4 м²

Характеристика материала:

Модуль упругости Е = 2,1 * 10¹¹ Па;
Коэффициент Пуассона ν = 0,3

Нагрузки:

Равномерно распределенная нагрузка q= 10 кН/м.

Результаты расчета:

Аналитическое решение:

При аналитическом решении прогиб в центре балки может быть вычислен по следующей формуле («Справочник по сопротивлению материалов» с. 352):

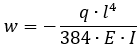
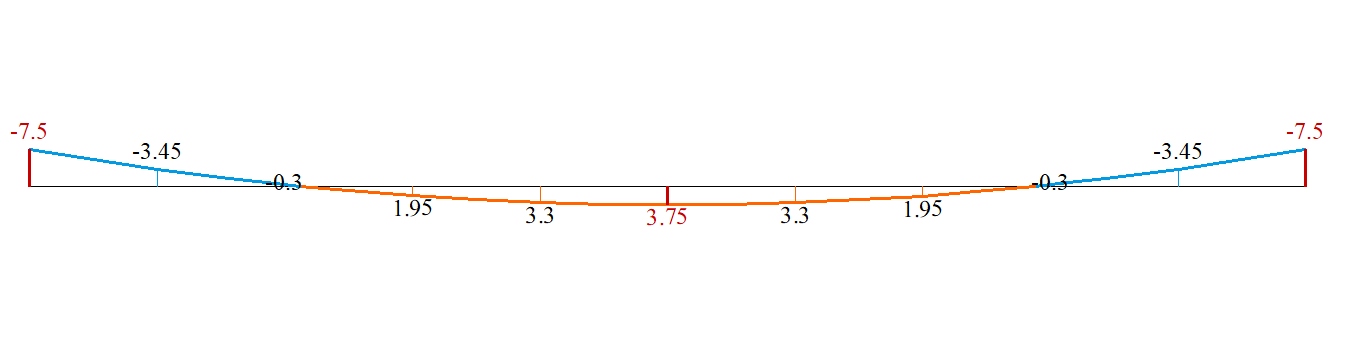
Изгибающие моменты в защемлении вычисляются по следующей формуле:

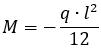
Изгибающий момент в центре балки:

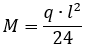
Сравнение результатов расчета:

Цель:

Определение напряженно деформированного состояния балки, защемленной с двух концов, от действия равномерно распределенной нагрузки, сосредоточенных продольных и поперечных сил и изгибающего момента.

Литература:

S. Timoshenko, Resistance des materiaux, t.1, Paris, Eyrolles, 1976, p. 26. M. Courtand et P. Lebelle, Formulaire du beton arme, t.2, Paris, Eyrolles, 1976, p. 219.

Формулировка задачи:

Определить вертикальное перемещение Z, продольную силу N и изгибающий момент M в середине пролета балки (точка G), а также горизонтальную реакцию на левом конце H (точка A).

Описание расчетной схемы:

Балка, защемленная с двух концов, нагружается равномерно распределенной нагрузкой P на всей длине пролета l, однонаправленными сосредоточенными продольными силами F₁ и F₂, расположенными на расстоянии 0,3l от левого и правого конца соответственно, сосредоточенной поперечной силой F, расположенной на расстоянии 0,3l от правого конца и сосредоточенным изгибающим моментом C, расположенным на расстоянии 0,3l от левого конца.

Геометрия:

Длина балки L = 1 м;
Момент инерции J = 1,7 * 10^-8 м⁴

Характеристика материала:

Модуль упругости Е = 2,0 * 10¹¹ Па;
Коэффициент Пуассона ν = 0,2

Нагрузки:

Значение равномерно распределенной нагрузки Р = 24 кН/м.;
Значение сосредоточенной силы F₁ = 30 кН;
Значение сосредоточенной силы F₂ = 10 кН;
Значение сосредоточенной силы F = 20 кН;
Значение сосредоточенного изгибающего момента C = 3 кН

Результаты расчета:

Сравнение результатов расчета: