Высокоточные конечные элементы с дополнительными узлами на сторонах

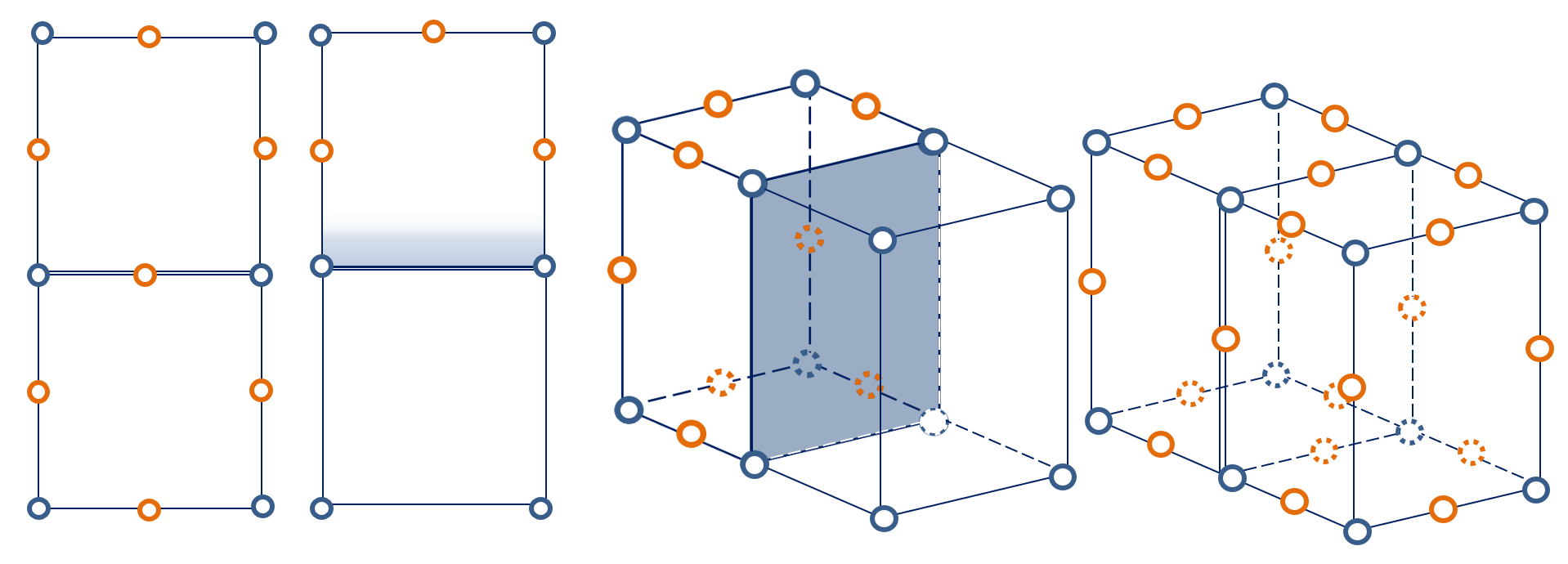
Начиная с версии ПК ЛИРА-САПР 2020 реализован механизм автоматического создания высокоточных (с узлами на сторонах) линейных конечных элементов.

• Тонкая плита и оболочка (по теории Кирхгофа-Лява);
• Толстая плита и оболочка (по теории Миндлина-Рейснера);
• Балка-стенка;
• Четырехугольная и треугольная призмы;
• Тетраэдр.

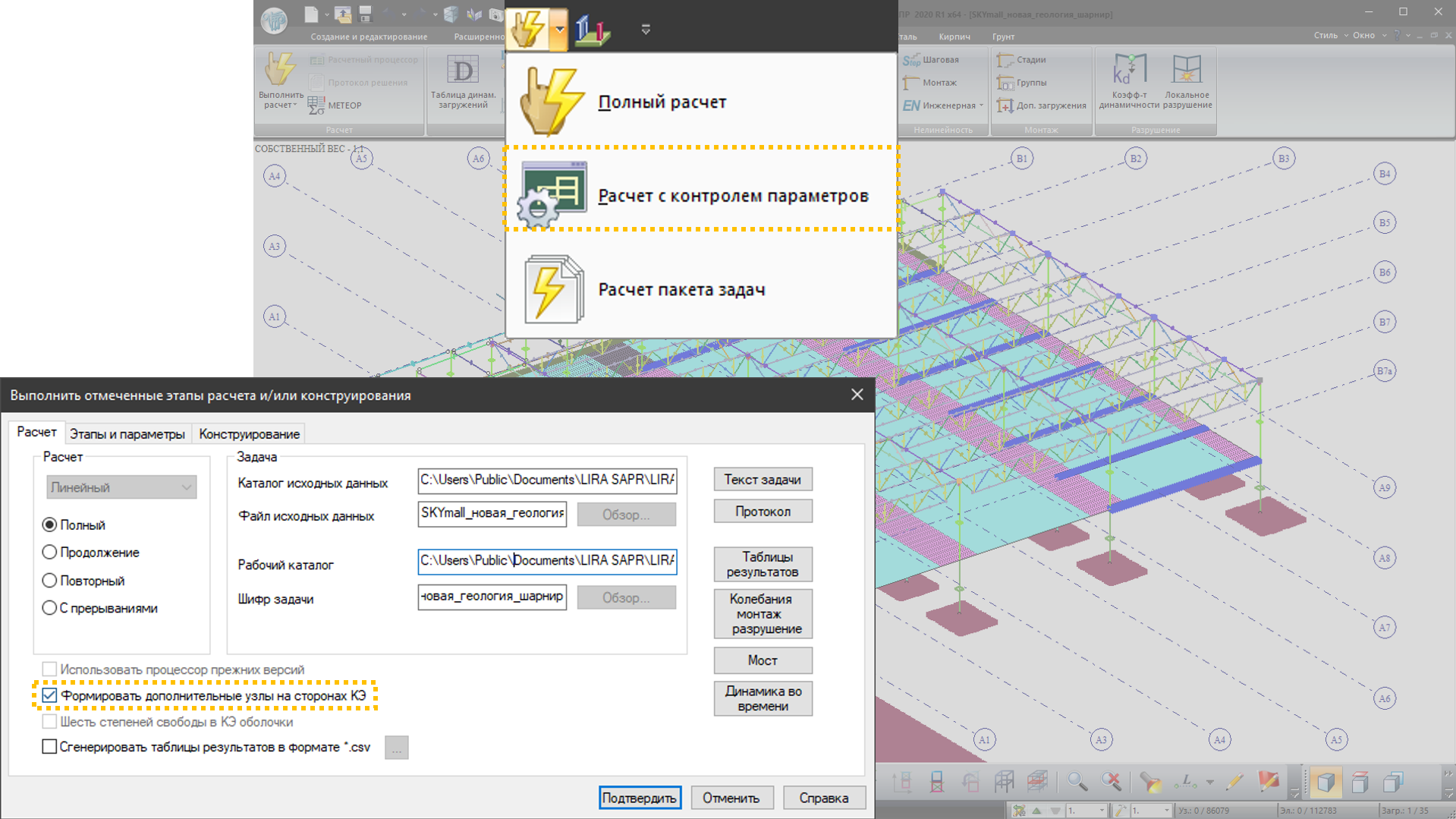
Промежуточные узлы на серединах ребер плоских и объемных высокоточных линейных конечных элементов, а также на серединах стержней, генерируются в процессе математического преобразования схемы непосредственно перед выполнением расчета. Для создания высокоточных КЭ в диалоговом окне Выполнить этапы расчета и/или конструирования на вкладке Расчет нужно установить флажок Формировать дополнительные узлы на сторонах КЭ (рис.2). Такой подход позволяет рассчитать задачу с более дробной сеткой КЭ, не переделывая схему инструментами редактирования.

Промежуточные узлы на серединах ребер плоских и объемных КЭ создаются только для тех элементов расчетной схемы, которые имеют высокоточные аналоги. Второй столбец таблицы содержит типы конечных элементов (по нумерации в библиотеке КЭ), для которых может создаваться высокоточный аналог.

*) Допускается учет ортотропии.

**) На каждом ребре пластины или объемного элемента может быть только 1 промежуточный узел. По правилам назначения дополнительных узлов высокоточные элементы могут иметь ребра без промежуточных узлов.

Элементы, для которых формируются промежуточные узлы, относятся к разряду высокоточных КЭ. Такими элементами могут быть только линейные КЭ.

Промежуточный узел не генерируется в случае, если:

• КЭ не имеет высокоточного аналога;
• к ребру или грани элемента примыкает элемент, который не имеет высокоточного аналога;
• на ребре элемента находится стержень с признаком Стержневой аналог;
• для любого из узлов элемента назначено Заданное смещение/поворот;
• для узлов ребра элемента назначены МСК с разнонаправленными осями.

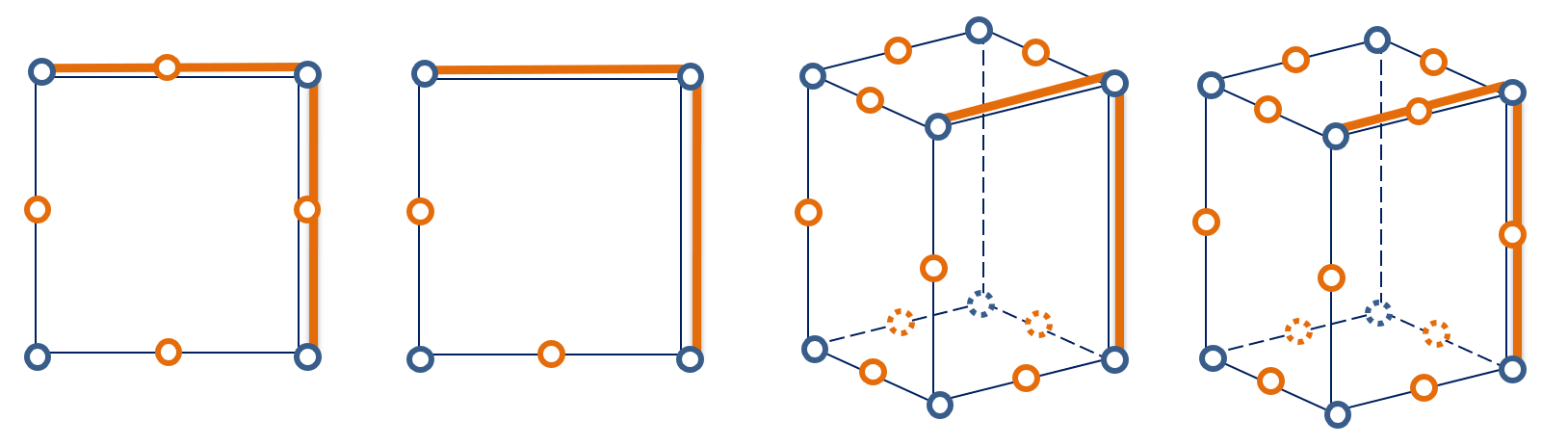
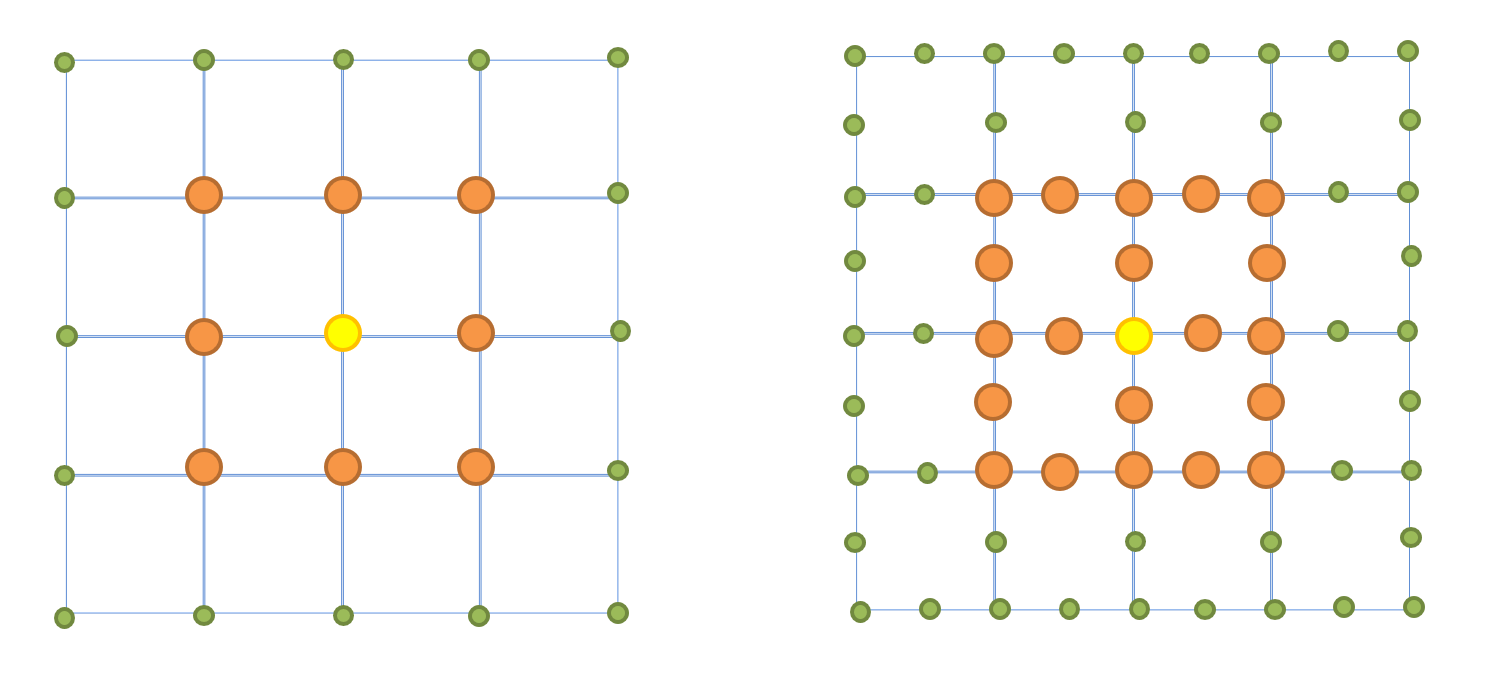
Сгенерированный узел является общим для всех элементов, ребра которых примыкают друг к другу.

Если стержневые КЭ 1...4, 7, 10 примыкают к ребру высокоточного КЭ, то на серединах стержневых элементов и на середине ребра высокоточного элемента генерируется промежуточный узел.

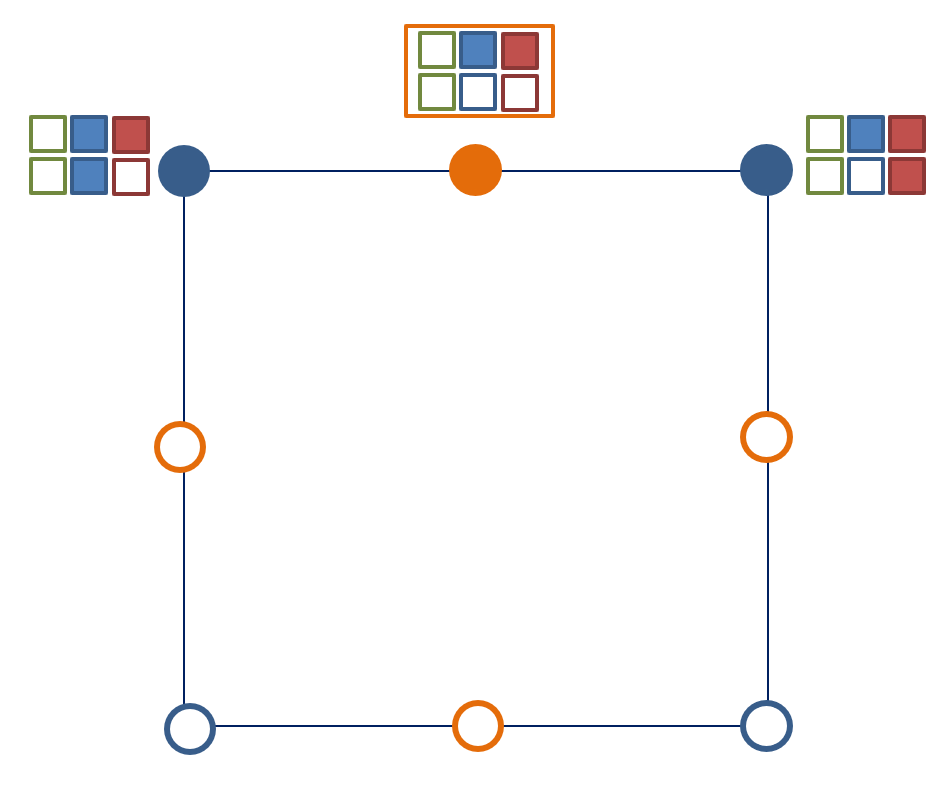
На промежуточный узел на грани элемента между двумя узлами с наложенными связями добавляются связи по совпадающим направлениям.

Промежуточный узел на грани элемента между двумя узлами, входящими в одно и то же АЖТ (абсолютно жесткое тело), включается в это же АЖТ.

Промежуточный узел на грани элемента между двумя узлами, входящими в одну и ту же группу объединения перемещений, включается в эту же группу.

Дополнительные узлы на схеме не визуализируются, результаты расчета (перемещения) для таких узлов не выводятся, но учитываются при вычислении усилий и напряжений в КЭ с промежуточными узлами.

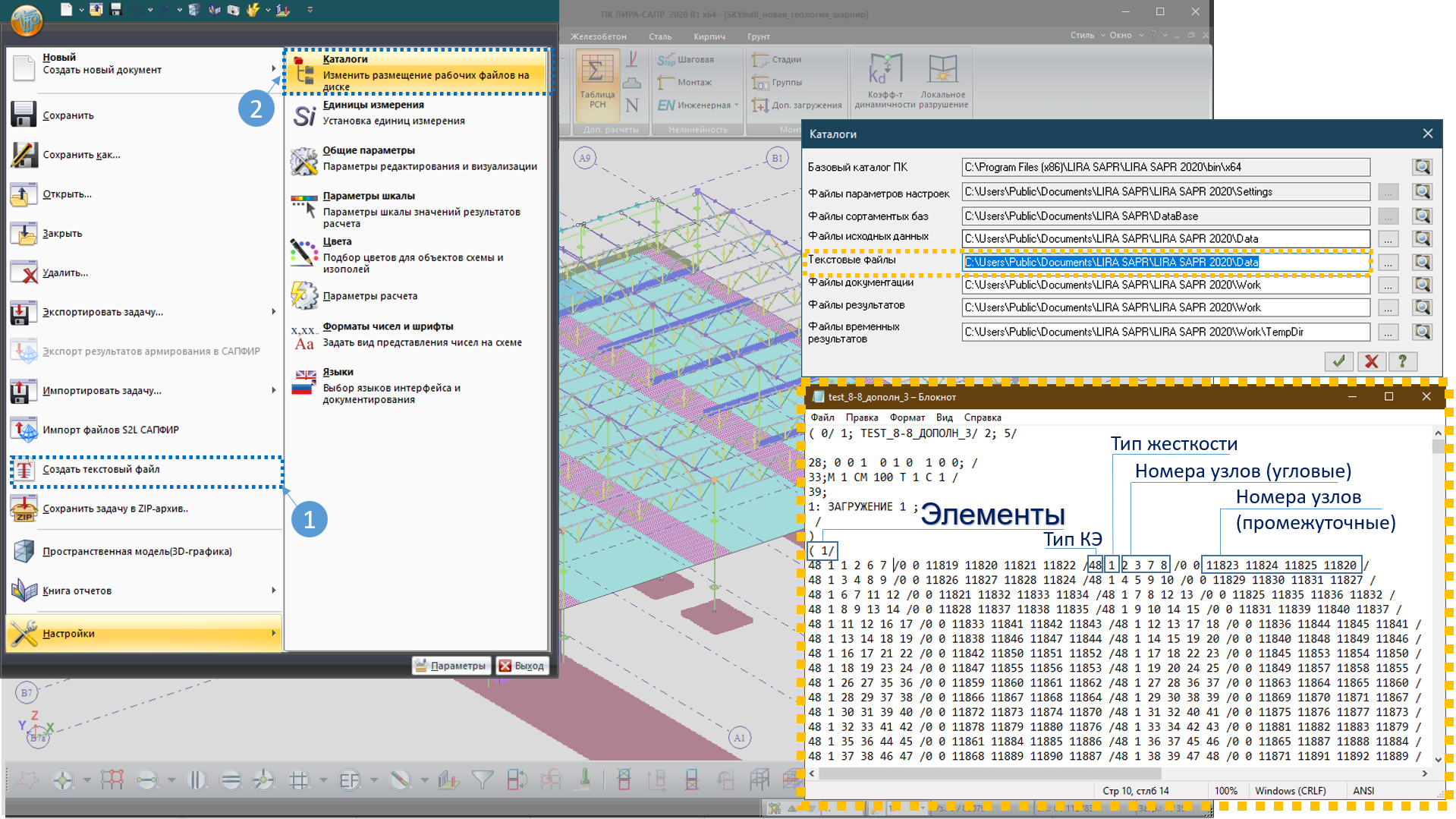
В текстовом файле задачи имеется информация о типе конечных элементов с промежуточными узлами. В строке с номером 1 указан тип КЭ (в данном случае – это высокоточный аналог 48, который создан на основе КЭ 44), далее – тип жесткости, номера узлов элемента. Сначала записываются номера узлов вершин (в зависимости от типа КЭ их количество может составлять от 3-х до 8-ми), далее – номера промежуточных, дополнительных узлов (от 1 до 20).

Следует учесть, что при установленном флажке Формировать дополнительные узлы на сторонах КЭ время разложения матрицы увеличивается.

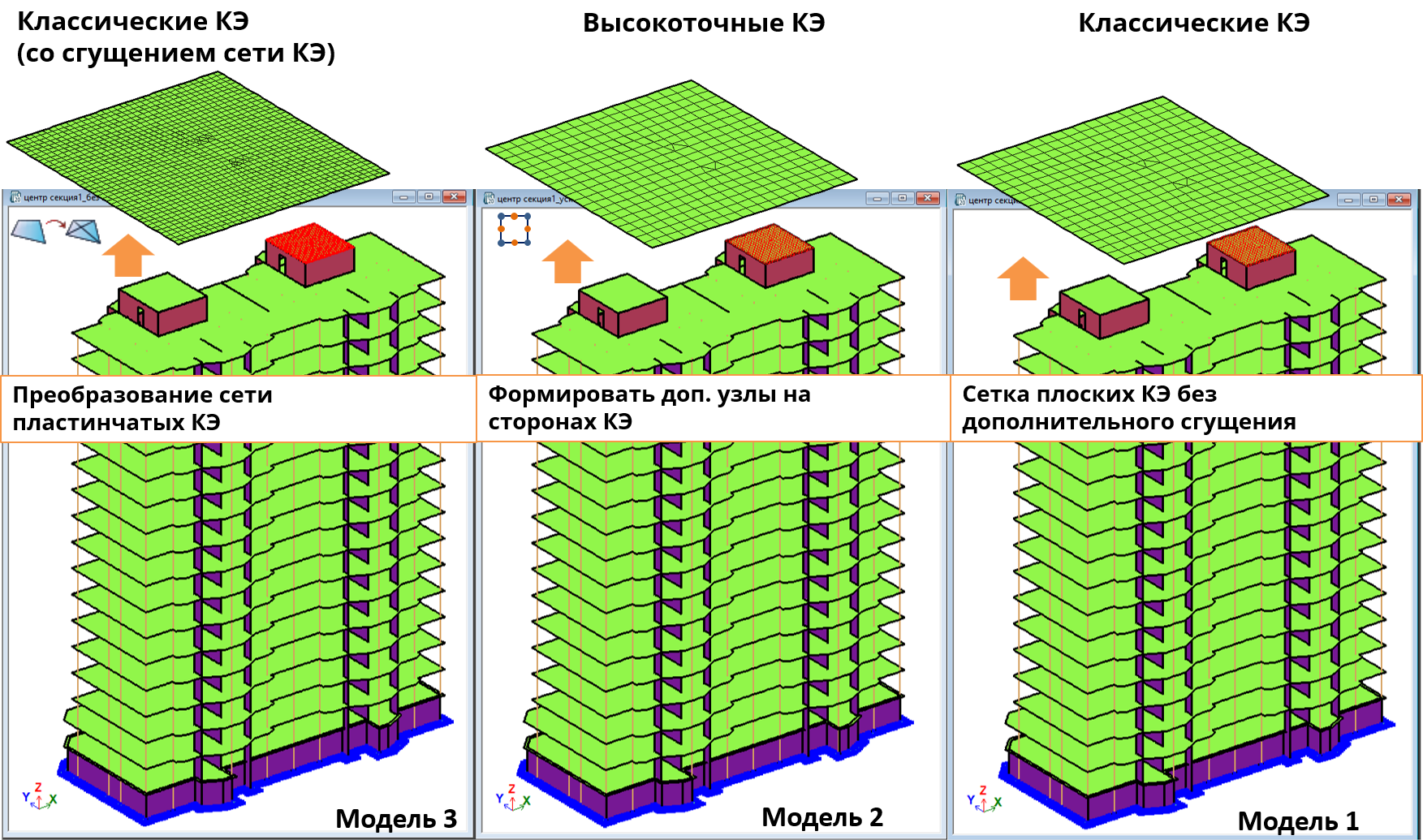
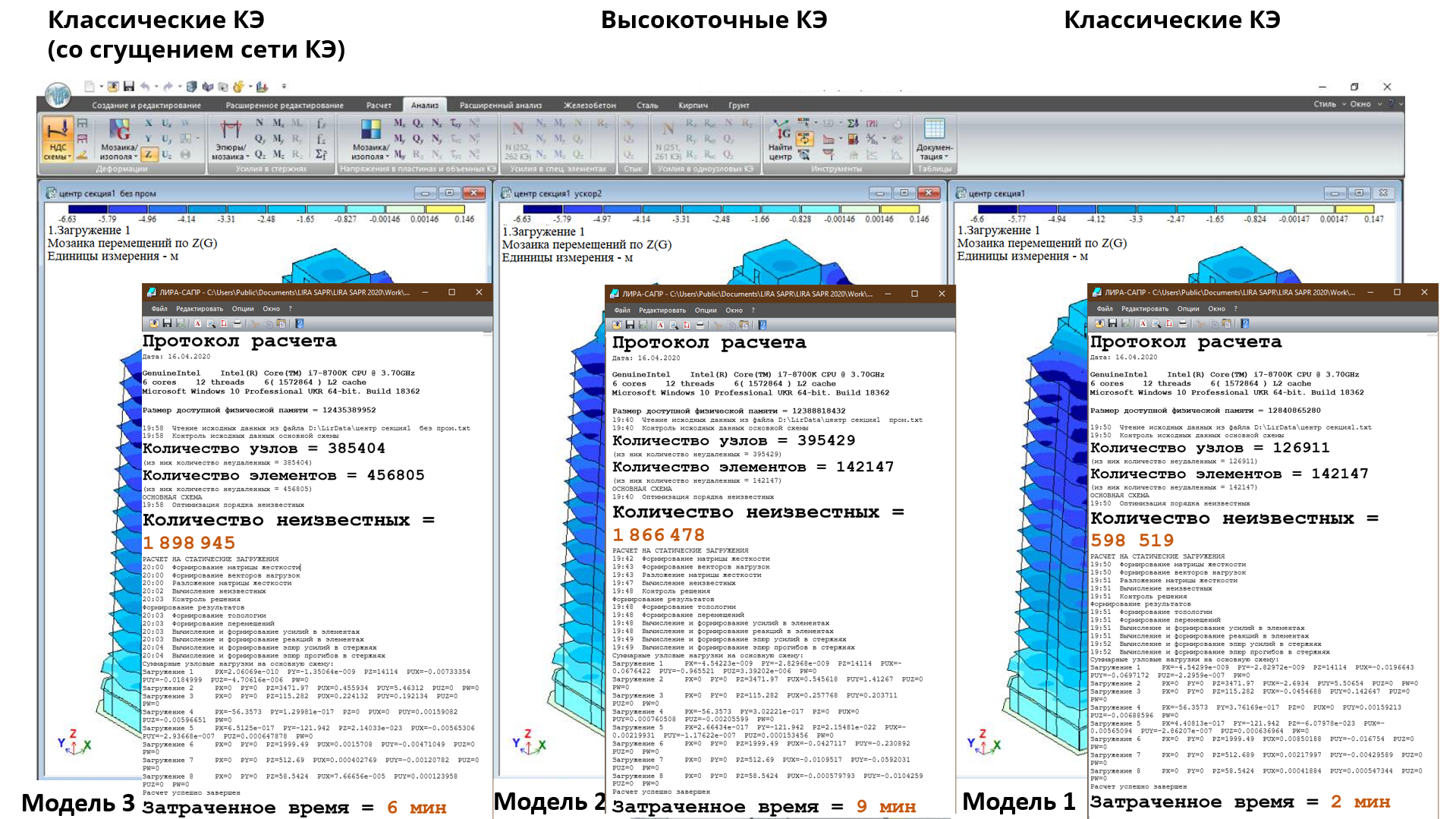
Для сравнения рассмотрим результаты трех тестовых задач. Модель 1 – базовая. Модель 2 получена из модели 1 при расчете с установленным флажком Формировать дополнительные узлы на сторонах КЭ. Модель 3 получена из модели 1 с помощью редактирования, а именно, сгущением сетки КЭ в 2 раза по двум направлениям.

Время разложения матрицы в задаче с промежуточными узлами (модель 2) в 1,5 раза больше, чем в задаче со сгущением сетки КЭ (модель 3), и в 5 раз больше, чем в задаче без сгущения сетки КЭ (модель 1).

Хотя количество неизвестных в задаче со сгущением сетки и в задаче с высокоточными элементами практически одинаково, на расчет задачи с высокоточными элементами тратится больше времени. Но следует отметить, что сгущение сетки вдвое приводит к меньшему увеличению точности, чем использование элементов с промежуточными узлами на сторонах. Это можно увидеть на верификационном примере.

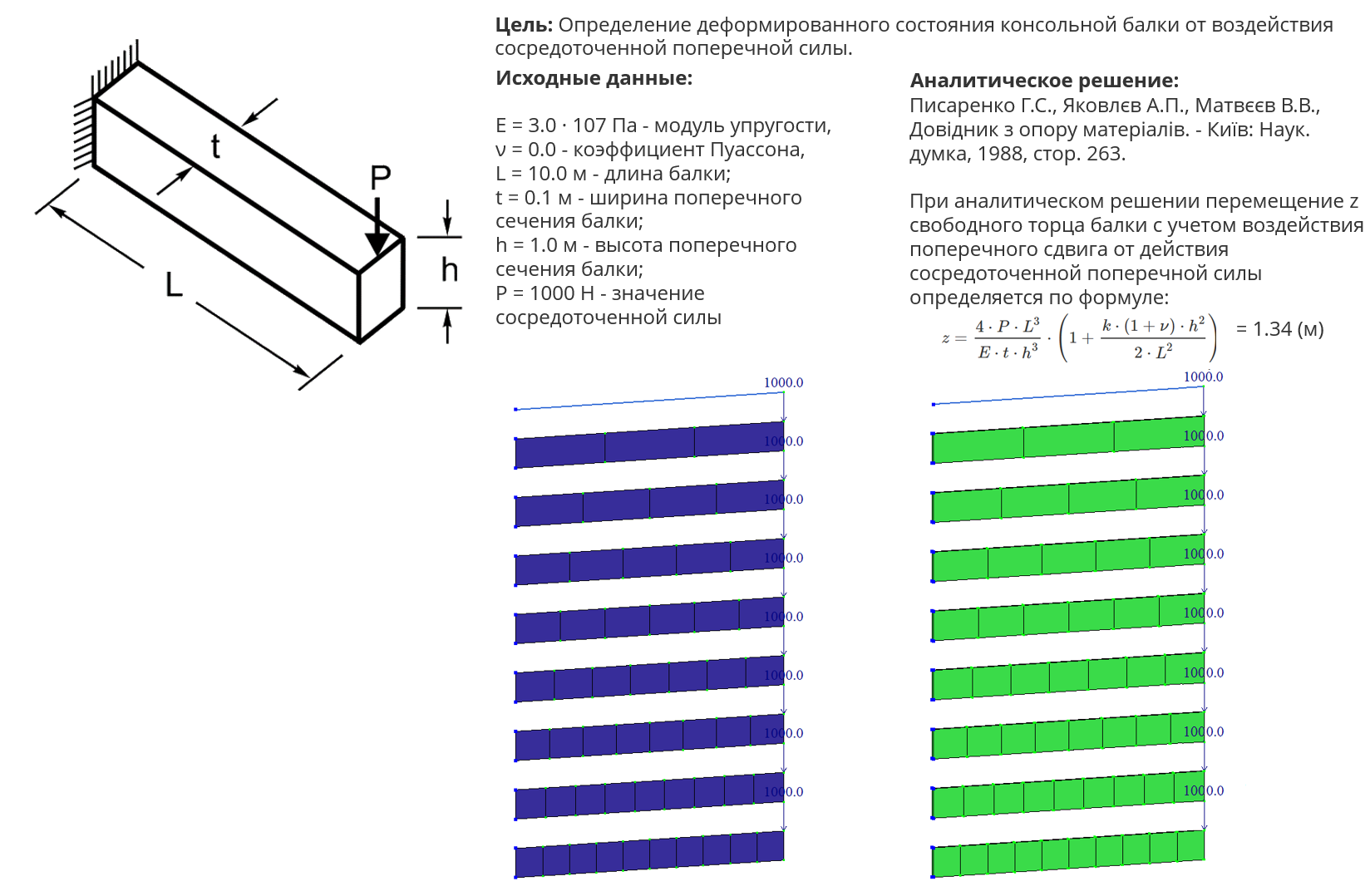
Рассмотрим задачу, которая имеет аналитическое решение: консольная балка под воздействием сосредоточенной поперечной силы.

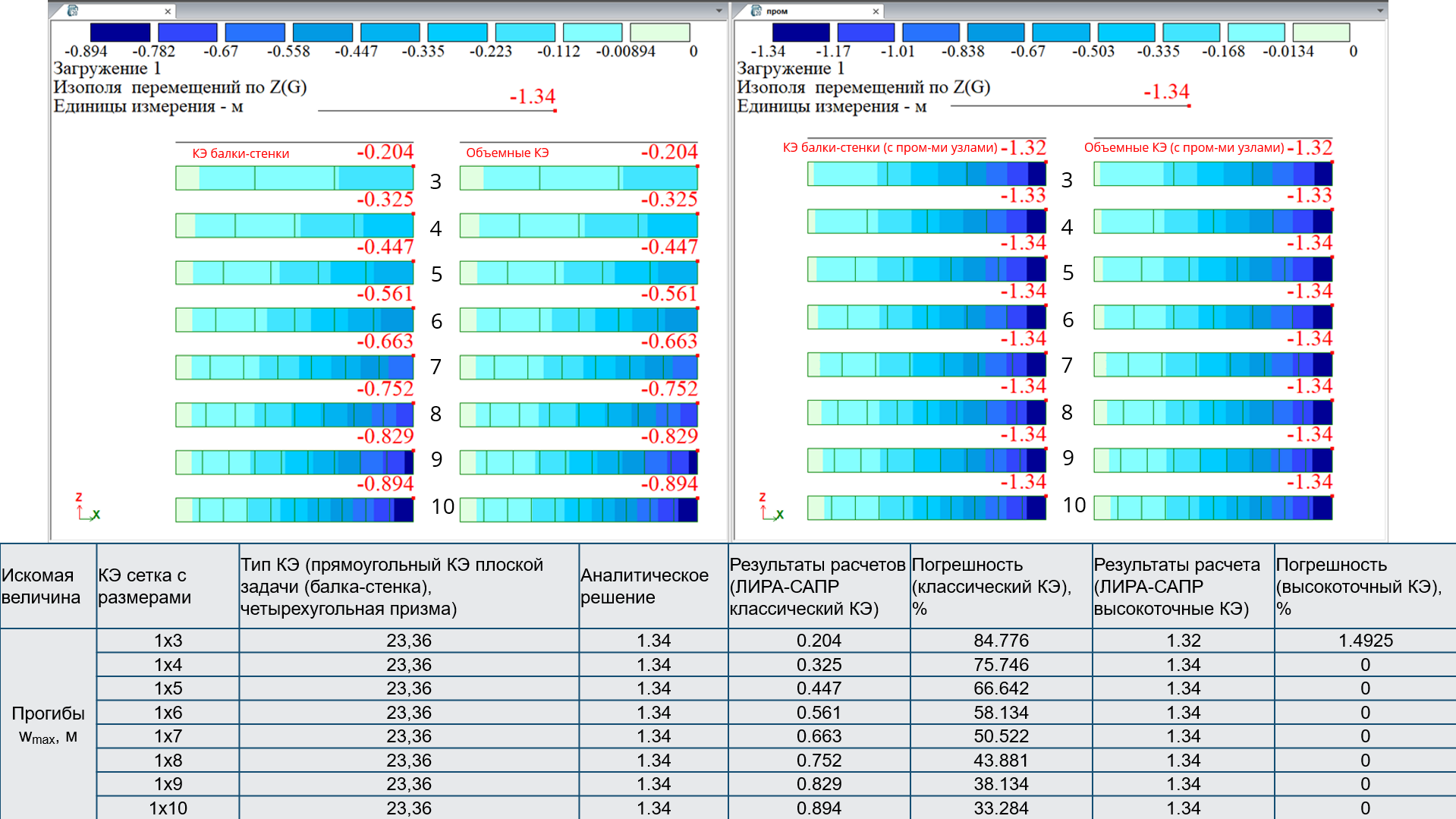
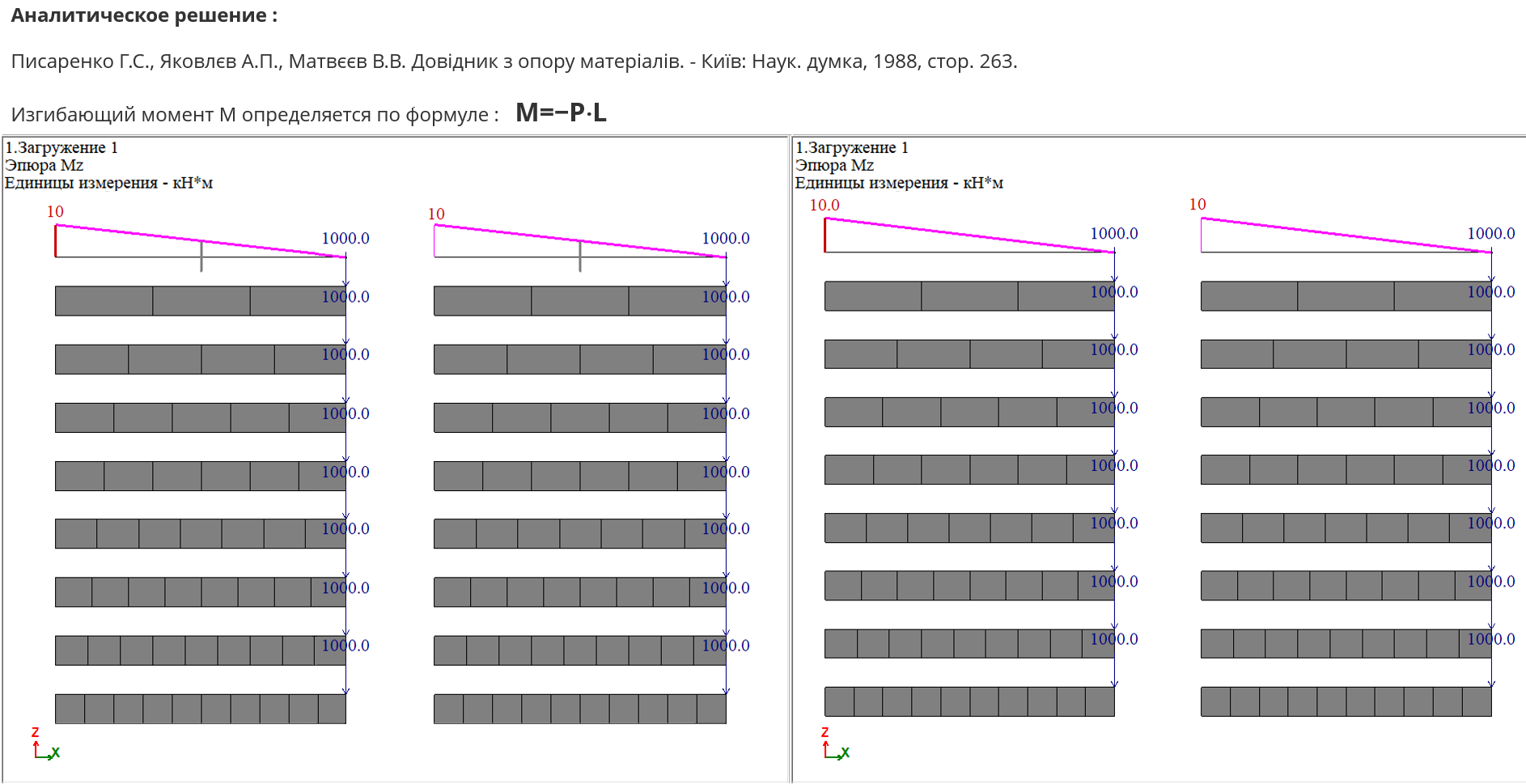
Создадим три модели балки. Модель 1 – базовая: балка смоделирована стержнем. Для модели 2 создадим балку из конечных элементов балки-стенки, для модели 3 – из объемных конечных элементов. Исследовать будем в двух направлениях: пошагово будем сгущать сетку КЭ и параллельно будем получать решение для этих же моделей, но с формированием дополнительных узлов на сторонах КЭ. Результаты исследования приведены в таблице на рис. 11.

Можно сделать вывод, что для данного примера в задаче с высокоточными КЭ необходимая точность достигается даже без сгущения сетки.