
Рассматриваются различные виды конструктивной нелинейности. Особое внимание уделяется проблеме односторонних связей. Приводится универсальный алгоритм расчета систем включающих односторонние связи. Приводится решение некоторых задач, для которых известные методы не приводят к необходимому результату.
Конструктивная нелинейность обуславливается свойством отдельных элементов конструкции включаться в работу в зависимости от различных факторов напряженно–деформированного состояния:
- усилия в элементе – элемент работает только на сжатие или на растяжение;
- элемент включается в работу после выбора зазора;
- элемент выключается из работы после достижения каких-либо факторов (например, после достижения предельного усилия).
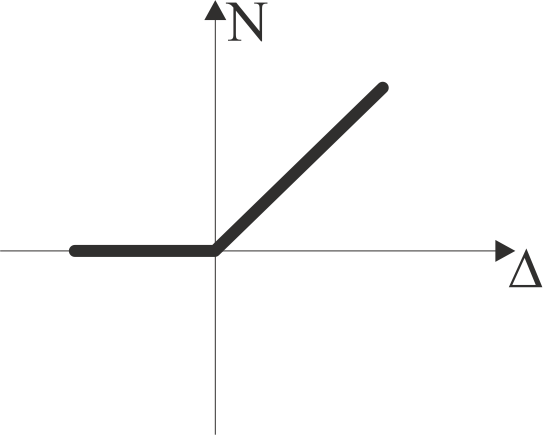
Конструктивная нелинейность может быть сведена к нелинейной зависимости между усилиями и перемещениями (рис. 1, 2):

|
|
|
а) |
б) |
|
Рисунок 1. Зависимости N – Δ для различных типов конструктивной нелинейности: а) элемент работает только на сжатие; б) элемент работает только на растяжение |
|

Рисунок 2. Зависимости N – Δ для различных типов конструктивной нелинейности: а) элемент включается в работу на растяжение после выбора зазора Δ1; б) элемент включается в работу на сжатие после выбора зазора Δ2; в) элемент работает только на растяжение и выключается из работы после достижения растягивающего усилия N1; г) элемент работает только на сжатие и выключается из работы после достижения сжимающего усилия N2.
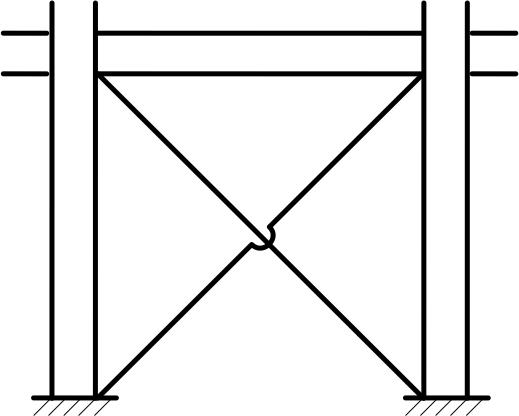
На рис. 3 а приведен пример вертикальных связей по колоннам промышленных цехов выполненных в виде двух непересекающихся тяжей, которые воспринимают только растягивающие усилия. Поэтому различным направлениям горизонтальной нагрузки соответствуют различные расчетные схемы (рис. 3 б, 3 в).
|
|
|
|
Рисунок 3. Конструктивная схема крестовых связей:
а) схема вертикальных связей; б) расчетная схема при нагрузке слева; в) расчетная схема при нагрузке справа
Зависимость N – Δ для тяжей в этом случае будет соответствовать рис. 1 б.
На рис. 4 представлена схема характерная для задач расчета зданий на подрабатываемых территориях. По мере обжатия грунта в работу будут включаться новые участки грунта. Зависимость N – Δ в этом случае будет соответствовать рис. 2 б.
Эту задачу можно отнести к классу контактных задач, которые часто встречаются в строительной практике.
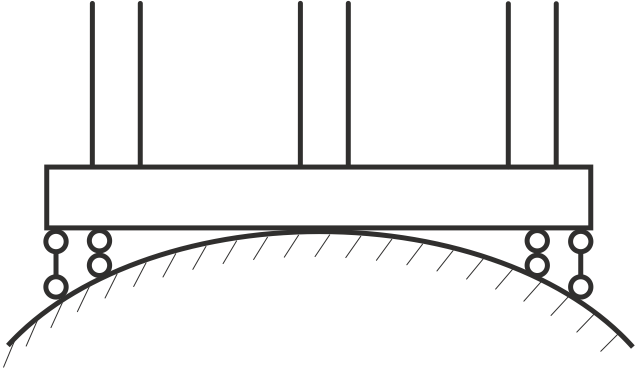
Рисунок 4. Фундаментная конструкция
на подрабатываемых территориях
На рис. 5 представлена схема характерная для фундаментов под высотные конструкции (башни, трубы, опоры ЛЭП, фундаменты под опоры ветроагрегатов и др.).
Конструкции фундаментов в этих случаях необходимо проверять на отрыв. Зависимость N – Δ для элементов моделирующих грунтовое основание соответствует рис. 1 а.

Рисунок 5. Фундаментная конструкция
высотных сооружений
На рис. 6 представлена схема характерная для конструкций мачт с вантами. Ванты работают только на растяжение и включаются в работу после определенного уменьшения провиса f. Зависимость N – Δ в этом случае будет соответствовать рис. 2 а. Наличие предварительного натяжения, которое практически всегда присутствует в конструкциях такого типа, несколько смягчает, но не исключает этот эффект. Предварительное натяжение обуславливает также возможность работы вант на определенную величину сжимающего усилия, примерно равную величине предварительного натяжения. После достижения этой величины ванта выключается из работы.

Рисунок 6. Конструкция мачты с вантами
Зависимость N – Δ в этом случае соответствует рис. 2 г. В ПК ЛИРА-САПР для решения задач подобного типа реализован шаговый метод.
Задачи с односторонними связями также относятся к классу задач конструктивной нелинейности.
Проблема расчета систем с односторонними связями (рис. 1 а, б) является достаточно сложной и ей уделялось и уделяется много внимания [1, 2, 3, 4, 5]. Наиболее естественный метод [1] расчета заключается в проведении ряда итераций, где на каждой последующей итерации исключаются связи с недопустимыми усилиями, полученными на предыдущей итерации. Такой метод часто приводит к зацикливанию, т.е. связи то включаются, то выключаются и путь к нахождению устоявшейся правильной окончательной схеме не может быть найден. В работе [3] приведен пример простейшей схемы (рис. 7) – все связи А, В, С работают только на сжатие – для которой приведенный выше метод приводит к зацикливанию.
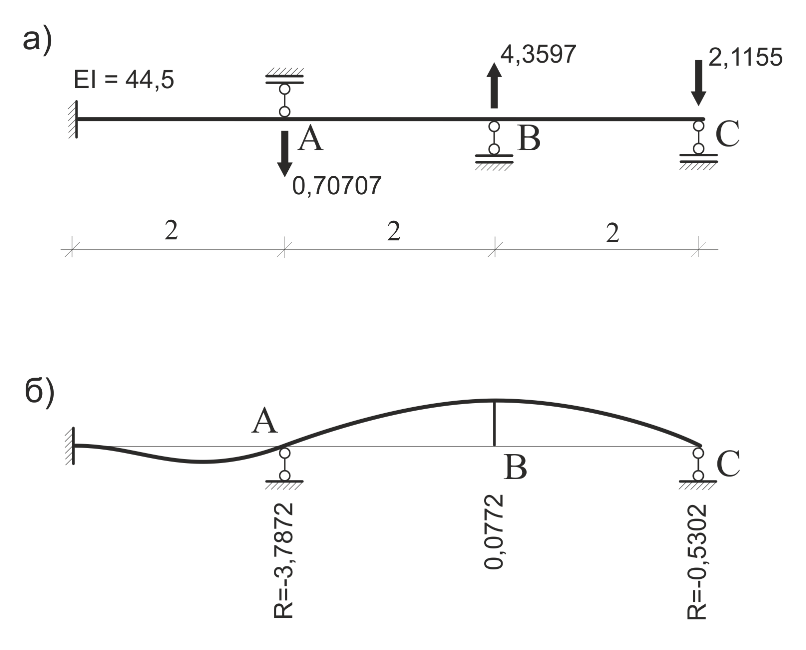
Рисунок 7. Тест № 1 а – рассчитываемая схема; б – точное решение
В ПК ЛИРА-САПР реализован численный итерационный метод решения подобных задач. В основу положен модифицированный метод компенсирующих нагрузок. В отличие от реализаций в устаревшем процессоре прежних версий ПК ЛИРА, в ПК ЛИРА-САПР происходит автоматический выбор количества итераций в зависимости от заданной точности. Критерием достижения заданной точности является квадратичная невязка между реакциями в связях на n+1 и n итерациях.
Пользователь по своему усмотрению сам может назначить количество итераций. В табл. 1 приведены результаты расчета схемы (рис. 7) в зависимости от количества итераций.
Таблица 1
|
Параметры решаемой задачи |
Точное решение |
Количество итераций |
||
|
2400 |
10000 |
30000 |
||
|
Реакция А |
3,7872 |
– 3,83 |
– 3,795 |
– 3,7871 |
|
Реакция С |
0,5302 |
– 0,52 |
– 0,527 |
– 0,5301 |
|
Перемещение В |
0,0772 |
0,0778 |
0,0773 |
0,0772 |
В работе [4] приведена схема (рис. 8) – все связи работают только на растяжение – которая при использовании метода [1] таит еще одну (кроме зацикливания) неприятность: уже после первой итерации схема превращается в геометрически изменяемую, и дальнейший расчет без каких-либо ухищрений невозможен.
На рис. 8 в приведено решение задачи итерационным методом (300 итераций), которое практически совпадает с точным решением. Элемент ABCD моделирован абсолютно жестким телом. ПК ЛИРА-САПР допускает применение в расчетных схемах произвольных абсолютно жестких тел с неограниченным количеством ведомых узлов. Решение большого количества практических задач итерационным методом ни разу не приводило к тупиковым ситуациям. Таким образом можно сделать осторожный вывод, что имеется универсальный алгоритм и программа для решения произвольных систем с односторонними связями.
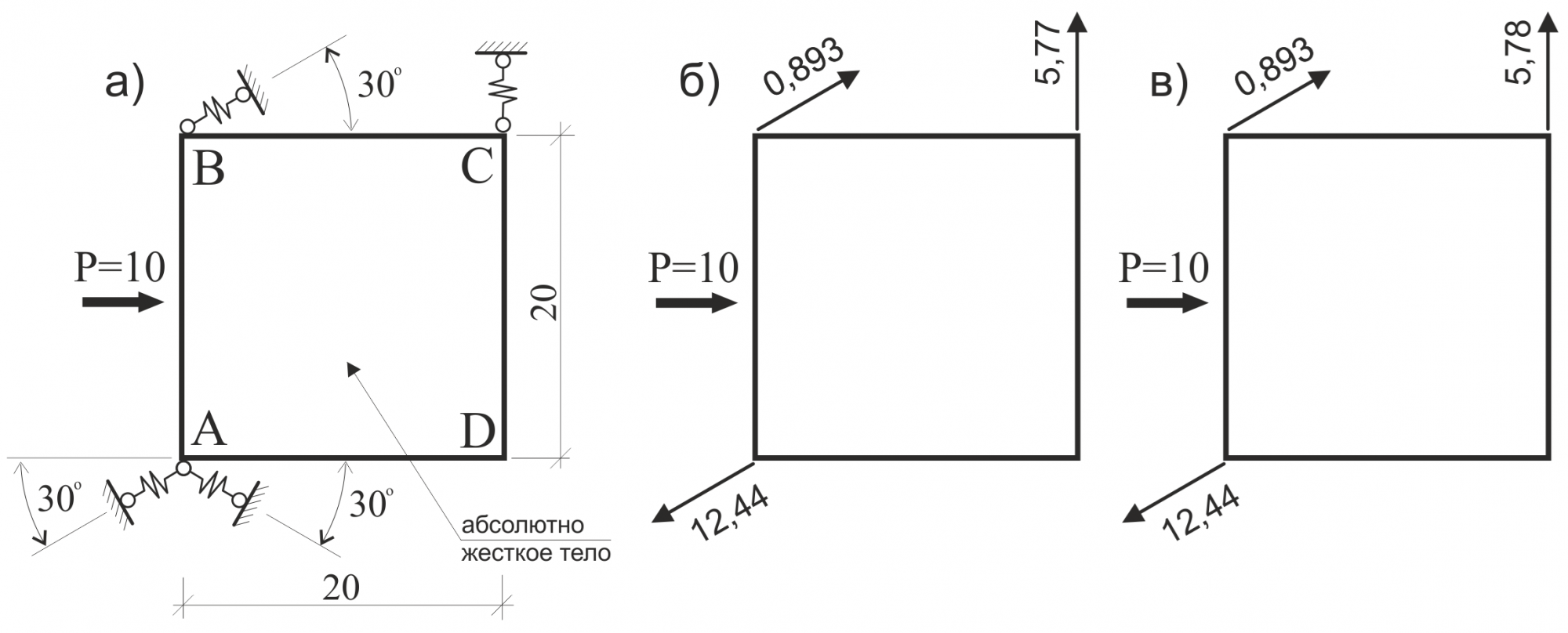
Рисунок 8. Тест № 2 а – рассчитываемая схема;
б – точное решение; в – решение, полученное итерационным методом
Литература
- Рабинович И. М. Некоторые вопросы теории сооружений, содержащих односторонние связи // Инженерный сборник – М. –Л.: Издательство АН СССР, 1950.– Т.VI.
- Гордеев В.И., Перельмутер А.В. Расчет упругих систем с односторонними связями, как задача квадратичного программирования // Исследования по теории сооружений. – М.:Стройиздат, 1966. – Вып. 15
- Перельмутер A. B. Элементы теории систем с односторонними связями // Обзоры по вопросам проектирования металлических конструкций. – М.: ЦИНИС Госстроя СССР, 1969. – Вып. 3. – 127 с.
- Перельмутер А. В., Сливкер В. И. Расчётные модели сооружений и возможность их анализа– М.: Издательство АСВ, 2011. – 709 с.
- Вовкушевский A. B., Шойхет Б. А. Расчет массивных гидротехнических сооружений с учетом раскрытия швов — М.: Энергоиздат, 1981. – 136 с.
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.







Комментарии