Глобальные, местные, локальные системы координат, углы чистого вращения

Модели и их компоненты в программном комплексе описываются в координатных осях следующих типов: глобальных, местных и локальных.

Это специфические понятия, связанные с особенностями формирования модели. Но предварительно укажем следующее: названные оси не является новой неизвестной системой координат. Речь идет о том, как связана модель в целом и ее компоненты с применяемой координатной системой (принята декартовая правая система).

Глобальная система координат (g) предназначена для задания общей геометрии системы – координат узлов, ориентации некоторых нагрузок, ориентации местных (m) и локальных (l) систем координат. Глобальная система координат может быть декартовой, сферической, цилиндрической или другой системой, которая может быть задана аналитически.

Глобальная декартова система координат обозначается в программном комплексе XYZ. Эта система принята по умолчанию, ее пиктограмма выводится в левом нижнем углу рабочего окна.

Местная система координат задается для конечного элемента и предназначена для ориентации конечного элемента относительно глобальной системы координат, удобства построения матрицы жесткости, задания местной нагрузки, определения напряжений и усилий. Как правило, местная система координат – декартова.

Все конечные элементы ПК ЛИРА-САПР, имеющие более одного узла (одноузловые КЭ также есть в программном комплексе) ориентированы в местной системе координат.

Локальная система координат (безусловно, здесь можно говорить о некоторой тавтологии – «местная» и «локальная», по сути, обозначают одно и тоже, однако будем считать, что это издержки терминологии) задается для узла и предназначена для ориентации некоторых его атрибутов: узловой нагрузки, узловых перемещений, наложенных связей. Как правило, локальная система координат тоже декартова. Реализации различных сочетаний этих систем предоставляет много удобств при составлении компьютерных моделей.

Пользователь ПК ЛИРА-САПР может манипулировать тремя типами систем координат в различных сочетаниях. Так, например, для гидростатического давления на цилиндрический резервуар удобно задавать местную нагрузку на конечные элементы в местной системе координат, а при нагрузке от собственного веса удобно задавать нагрузку в глобальной системе координат. Если необходимо задать узловую нагрузку, связь, или организовать расчет на заданное перемещение, направление которых не совпадает с осями глобальной системы, то в соответствующий узел вводится локальная система координат с нужными направлениями.

Алгоритмы построения матриц жесткости (МЖ) и приведение местной нагрузки к узловой удобно организовывать в местной системе координат. Это касается как использования аналитического вида МЖ (для каждого элемента МЖ имеется формула) так и при численном интегрировании. Для ориентации местной системы координат КЭ имеющих более двух узлов достаточно иметь координаты трех узлов.

Например, ось Х_m проводится через первые два узла (рис. 2), ось Y_m совпадает с направлением перпендикуляра к оси X_m, проходящего через третий узел, а ось Z_m образует правую тройку.

При этом матрица направляющих косинусов (Cmg), на основе которой производится перевод атрибутов КЭ (матрица жесткости, местная нагрузка и др.) из местной системы координат в общую имеет вид:

Компоненты этой матрицы вычисляются по координатам трех узлов элемента (см. рис 2) в глобальной системе координат по следующим формулам:

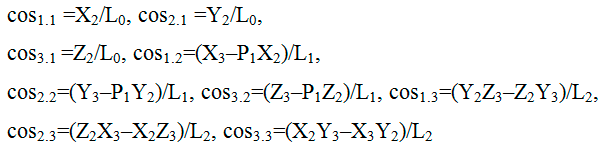
где  – длина отрезка 1–2,

 – длина перпендикуляра из узла 3 на 1–2, , 

X₂, Y₂, Z₂, X₃, Y₃, Z₃ – координаты в глобальной системе 2 и 3 узлов относительно узла 1, т.е. X₂=X₂ – X₁ и т.д.

Для двухузловых элементов, а их класс очень велик (стержневые элементы), координат двух узлов недостаточно для построения такой матрицы косинусов, для этого еще необходима дополнительная информация, например, угол чистого вращения, определяющий положение главных осей сечения стержня относительно глобальной системы координат (рис. 3).

Как правило, ось X_m совпадает с осью стержня (рис. 3а), а оси Y_m и Z_m являются главными осями сечения стержня. Обычно их ориентация определяется углом чистого вращения (устоявшийся термин строительной механики стержневых систем), который является углом между одной из главных осей сечения (например, Y_m) и осью ОА (пересечение плоскости поперечного сечения стержня, которая ортогональна оси X_m, с плоскостью Х0Y глобальной системы координат).

Очень часто направление Y_m задают третьим узлом, тогда построение Cmg для стержня аналогично элементу пластины.

Для задания локальной системы координат необходимо задание матрицы Clg направляющих косинусов между осями локальной и глобальной систем координат. Если матрица Cmg для элементов, имеющих более двух узлов может быть построена на основе имеющихся координат узлов, заданных в глобальной системе координат, то при задании Cmg для стержня, а также Clg нужна дополнительная информация, поэтому программный комплекс должен предоставлять пользователю удобный инструментарий для его задания.

При составлении канонических уравнений МКЭ матрицы жесткости K_m и векторы местной нагрузки Р_m, приведенной к узловой, необходимо переводить в глобальную систему координат, а если узел имеет локальную систему координат, то этот перевод необходимо произвести с учетом локальной системы координат. Этот перевод производится по следующей схеме:

С_mg – матрица косинусов для перевода компонентов K_m и Р_m из местной в глобальную систему координат;

С_gl – матрица косинусов для перевода компонентов K_m и Р_m из глобальной в локальную систему координат.

Очевидно, что 

Кроме того, 

Тогда для перевода вектора из местной системы координат в локальную используется матрица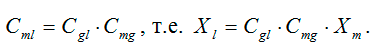 

Для преобразования матрицы жесткости в местной системе координат K_m в матрицу жесткости в локальной системе координат K_l

Для вектора правых частей:

Для преобразования K_m в матрицу жесткости относительно глобальной системы координат используется формула:

, a для вектора правых частей 

Перевод параметров НДС из одной системы координат в другую производится во многих случаях, например, вычисленные в местной системе координат напряжения (усилия) перед построением изолиний и изополей должны быть переведены в глобальную систему, а при построении главных напряжений должны быть указаны их направления относительно глобальной системы координат и т.п.

• глобальная система координат
• локальная система координат
• местная система координат
• матрица жесткости