LIRALAND

Test 1.14. Compression and bending of a wedge by a concentrated force (Mitchell problem)

Updated Feb 09, 2026 | Published Oct 18, 2025

Objective

To determine the stress state of a symmetric wedge of unit thickness subjected to compression and bending by concentrated forces.

Reference

Demidov S.P. Theory of Elasticity, Moscow, Vysshaya Shkola, 1979.

Problem statement

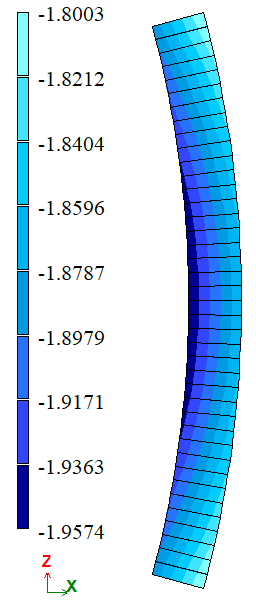
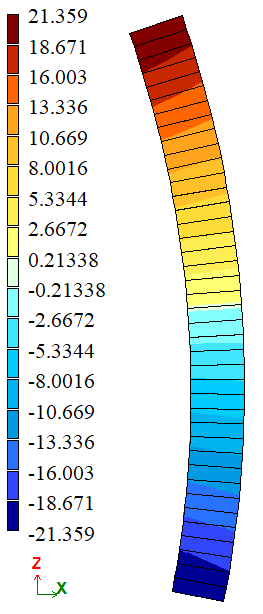
To determine the radial stress σrr in polar coordinates at a distance r = 5 m from the wedge apex.

Design model

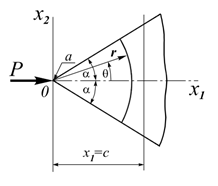
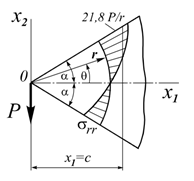
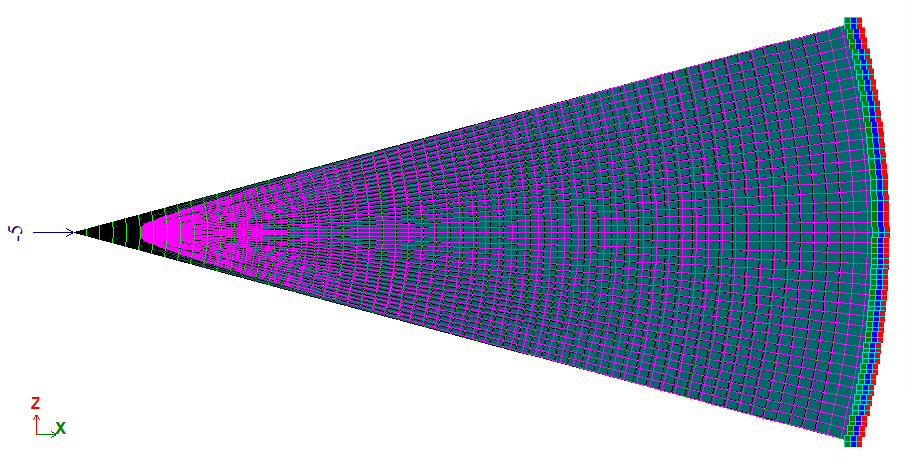
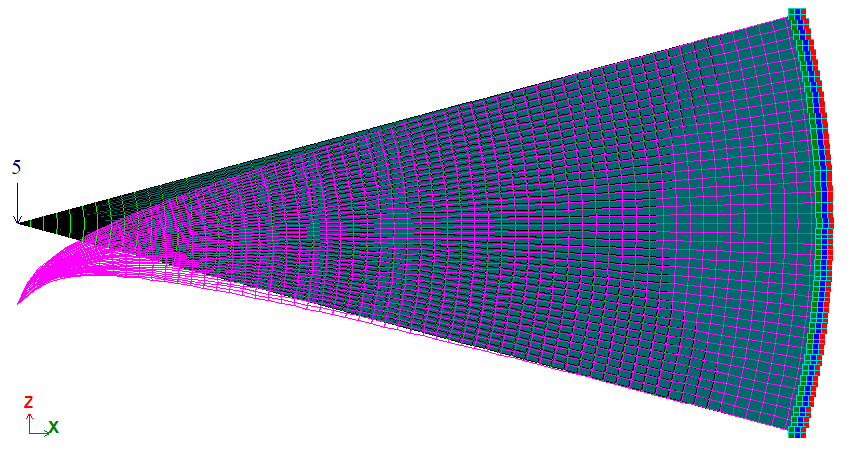
A force P is applied to the apex of a wedge of unit thickness acting as follows:
Variant 1: along the axis of symmetry of the wedge;
Variant 2: perpendicular to the axis of symmetry of the wedge.

Initial geometry of analytical model, variant 1

Initial geometry of analytical model, variant 2

Variant 1

Variant 2


Initial geometry of analytical model

Initial geometry of FE model, variant 1

Initial geometry of FE model, variant 2

Variant 1

Variant 2


Initial geometry of FE model

Geometry

Wedge thickness h = 1 m
Radius limiting the wedge domain R = 15 m
Wedge apex angle 2α = 30°

Material properties

Modulus of elasticity Е = 3 * 107 kPa
Poisson's ratio ν = 0,2.

Boundary conditions

Restraints in all degrees of freedom along the wedge arc contour.

Loads

Concentrated load Р = 5 kN

Output data

Design and deformed shapes, variant 1

Design and deformed shapes, variant 2

Variant 1

Variant 2


Design and deformed models

Stress contour plot σrr (Ny), kN/m2, variant 1

Stress contour plot σrr (Ny), kN/m2, variant 2

Variant 1

Variant 2


Stress contour plot σrr (Ny), kN/m2 (model fragment)

Analytical solution

Variant 1:

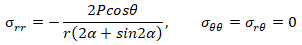
Variant 2:

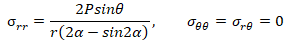
Comparison of calculation results

Without additional side nodes:

Point The unknown Analytical solution LIRA-FEM Error, %
r = 5 m Var. 1 σrr.max, kN/m2 -1,88 -1,8003 4,2394
σrr.min, kN/m2 -1,95 -1,9574 0,3781
Var. 2 σrr.max, kN/m2 21,8 21,359 2,0229
σrr.min, kN/m2 -21,8 -21,359 2,0229

With additional side nodes:

Point The unknown Analytical solution LIRA-FEM Error, %
r = 5 m Var. 1 σrr.max, kN/m2 -1,88 -1,8006 4,2234
σrr.min, kN/m2 -1,95 -1,9578 0,3984
Var. 2 σrr.max, kN/m2 21,8 21,442 1,6422
σrr.min, kN/m2 -21,8 -21,442 1,6422

Download verification test

Download

If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.

  • 14

Comments

Write