Учет нелинейной работы железобетона в ПК ЛИРА-САПР. Метод «Инженерная нелинейность»

В статье рассматривается итерационный метод «инженерная нелинейность». Представляемый метод позволяет определить реальные жесткостные характеристики сечения, которые могут быть пониженными  в связи с появлением трещин, пластическими деформациями бетона и арматуры.

Предлагаемый метод «инженерная нелинейность», с одной стороны позволяет более точно учитывать распределение жесткостей, с другой стороны по технологии практически аналогичен традиционным методам расчета в линейной постановке, т.е. позволяет выполнить расчет на все нагружения, получить РСУ и РСН, подбор арматуры.

 

Постановка задачи

Ползучесть, трещины и другие специфические особенности железобетона обуславливают изменение жесткостных характеристик элементов уже на ранних этапах нагружения, включая и эксплуатационную стадию. Это приводит к перераспределению усилий, значительному увеличению перемещений по сравнению с линейно-упругим расчетом. Нормативные документы ориентируют инженера на учет этих факторов. Так в Еврокоде и нормативах Российской Федерации рекомендуется проводить расчет с учетом физической нелинейности. Программный комплекс ЛИРА-САПР предоставляет возможность инженеру выполнять такие расчеты. Однако расчет конструкции с учетом физической нелинейности [2, 3, 6] в строгом математическом понимании этого процесса при использовании в массовых инженерных расчетах имеет ряд недостатков:

• такой расчет может быть выполнен только на одно нагружение и его нельзя использовать в РСУ или РСН;
  
• такой расчет требует больших ресурсозатрат – шаговый метод обуславливает необходимость многократного решения систем линеаризованных уравнений;
  
• такой расчет требует задания арматуры (диаметры и расположение) в каждом сечении стержня или пластинчатого элемента.
  

С другой стороны, нормативы Российской Федерации СП 52-103-2007, для учета этих факторов в инженерных расчетах, предлагают просто вводить понижающие коэффициенты на жесткость для изгибаемых элементов 0,3 и сжатых 0,6. Конечно, такое грубое предположение не учитывает, что снижение жесткости зависит от величины и характера напряженного-деформированного состояния сечения. О снижении жесткости растянутых элементов вообще ничего не говорится.

Такой подход достаточно грубо оценивает действительную ситуацию. Это можно продемонстрировать на примере элементарной защемленной балки (рис.1).

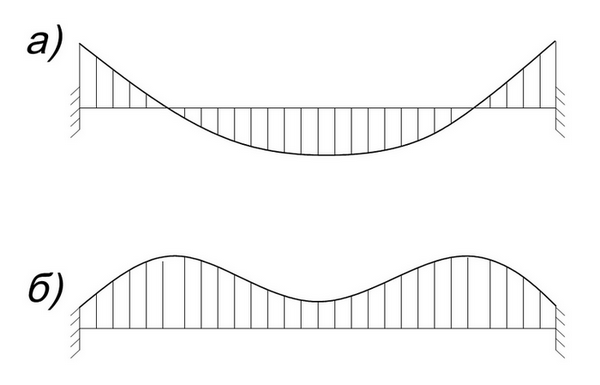
В реальных расчетах ситуация еще более сложная. Колонны зачастую испытывают значительные нормальные усилия: балки испытывают значительные изгибное усилие; в пластичных элементах как правило возникают соизмеримые мембранные и изгибные усилия.

Метод «Инженерная нелинейность» ориентирован на некоторое устранение этого несоответствия (некоторые идеи в этом направлении предлагались ранее [1]) и этот метод надо позиционировать как метод уточненного дифференцированного учета снижения жесткостных характеристик железобетонных элементов.

Концепция метода

Метод «Инженерная нелинейность» состоит в следующем:

1. Задается «определяющее нагружение», которое по мнению инженера в основном определяет напряженно-деформированное состояние конструкции (развитие трещин, пластические деформации бетона и арматуры) на протяжении жизненного цикла конструкции. «Определяющее нагружение» может составляться на основании набора нагружений (собственный вес, полезные нагрузки и др.), которые задаются инженером для последующего традиционного расчета или назначается инженером на основе других предположений.
   
2. Производится расчет на «определяющее нагружение» в физически нелинейной постановке с одновременным подбором арматуры. Расчет выполняется итерационным методом и производится подбор арматуры.
   
3. В результате итерационного расчета на основе НДС каждого сечения стержня и КЭ пластинчатой конструкции определяются жесткостные характеристики.
   
4. Выполняется традиционный расчет конструкции, элементы которой имеют жесткостные характеристики определяемые в результате итерационного расчета. Традиционный расчет подразумевает расчет в линейно-упругой постановке на весь набор нагружений (собственный вес, полезная нагрузка, сейсмика и др.), составление РСУ или РСН, подбор или проверку сечений стержней железобетонных и стальных элементов, конструирование.
   

Наиболее ответственным и сложным в постановке и реализации является этап определения жесткостных характеристик сечений стержня и пластинчатого элемента [4,5].

Определение жесткостных характеристик сечения стержня

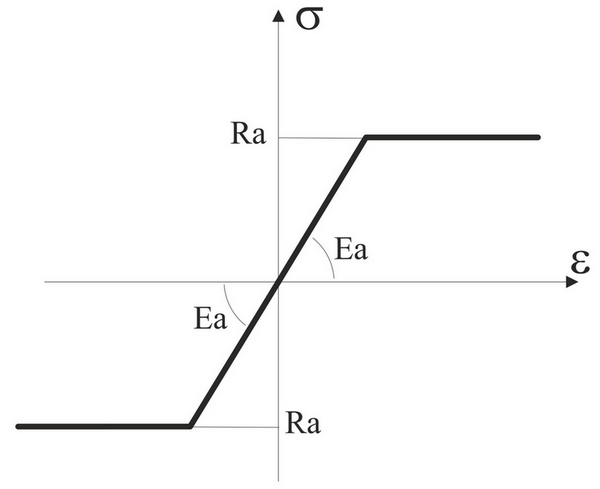
На рис. 2 представлено произвольное сечение стержня, на которое действует два момента Mx и My, нормальная сила N. Моменты действуют относительно главных осей сечения x и y. Нормальная сила приложена в точке С – пересечении геометрической оси стержня с плоскостью сечения. Требуется: определить жесткостные характеристики сечения, соответствующие секущим модулям деформаций бетона и арматуры.

Зависимость  для бетона представлена на рис. 3, для арматуры – на рис. 4.

Для определения НДС сечения необходимо найти положение нейтральной оси, которое характеризуется двумя величинами ,  и кривизной сечения  (рис.2):
– смещение нейтральной оси;
  – угол поворота нейтральной оси;
  – кривизна сечения.
Решение задачи выполняется численным методом. В результате итерационного процесса определяются три неизвестных , , , которые находятся из трех уравнений равновесия: 

Здесь – элементарные участки, на которые расчленяется сечение бетона и площади отдельных стержней арматуры.

n – количество участков бетона, m – количество арматурных стержней.

 

– секущие модули деформаций бетона и арматуры, которые определяются на основании зависимостей  (рис. 2,3).

Х_jб, Y_jб, X_ia, Y_ia – расстояние центра тяжести j-го участка бетона и i-го участка арматурного стержня до главных осей, положение которых (, ) определено в результате итерационного расчета.

Для бетона в определение входит только сжатая часть бетона с переменным по сечению секущим модулем деформации. Для каждого арматурного стержня также используется соответствующий секущий модуль деформации.

Матрица жесткости стержня, имеющего переменные по длине секущие жесткостные характеристики (рис.1) также строится численным методом (каждый стержень рассматривается как своеобразный супер элемент).

Примеры применения

Ниже приводятся результаты расчета рамы на основе инженерной нелинейности (рис. 4).

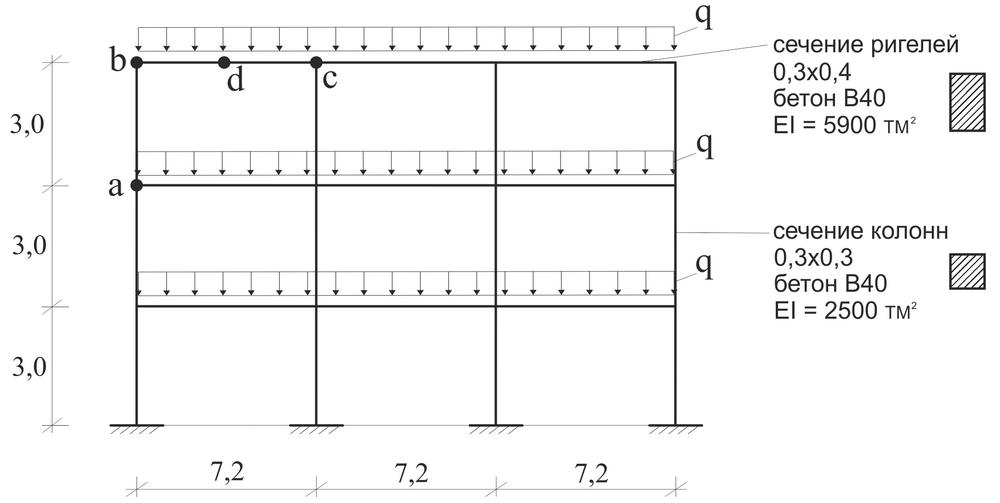
В качестве определяющего нагружения была принята нагрузка q=15 т/п.м. на рис. 6 приведены соответствующие жесткости для ригеля b – с и колонн а – b.

Анализируя эпюры жесткостных характеристик можно сделать вывод, что рекомендуемое нормативами снижение жесткостных характеристик для колонн на понижающий коэффициент 0,6 (в этом случае эпюра для колонн выглядела бы постоянной и равной 0,6х2500=1500 тм²) и для ригелей 0,3 (в этом случае эпюра выглядела бы постоянной и равной 0,3х5900=1770 тм²) выглядит достаточно грубым приближением.

В таблице 1 приведены результаты линейно-упругого расчета рамы на нагрузку q=20 т/п.м. с учетом дифференцированного распределения жесткостей для всех элементов, полученных на основе режима «Инженерная нелинейность».

Таблица 1. Результаты линейно-упругого расчета рамы.

Анализируя результаты расчета приведенные в табл. 1 можно сделать следующие выводы:

• получено некоторое перераспределение усилий – в менее нагруженном сечении «b» ригеля момент увеличился, в более нагруженном сечении «d» ригеля момент уменьшился;
  
• перемещение узла «d» увеличилось более чем в 2 раза;
• частота собственных колебаний (первая форма) уменьшилась, а период увеличился.
  

Отображение мозаик интегральных жесткостных характеристик

Для расчета железобетонных конструкций с использованием инженерной нелинейности в ЛИРА-САПР введено построение мозаик интегральных жесткостных характеристик стержней и пластин. Мозаики интегральных жесткостей можно включить из выпадающего меню «Усилия» в результатах расчета.

Пример мозаики интегральной изгибной жесткости для пластинчатых элементов: в местах изгибающих моментов близким к нулю (на шарнирной опоре справа и на расстоянии 1/4 пролёта от опоры с защемлением) наблюдается локальное увеличение жесткости сечения. В остальных местах плиты жесткость снизилась.

Пример мозаики интегральной изгибной жесткости для стержневых элементов: обратите внимание – в местах, где эпюра моментов в ригеле пересекает ноль наблюдается увеличение изгибной жесткости, по сравнению с начальной жесткостью линейного сечения с начальным модулем упругости бетона. Это связано с тем, что при расчете интегральных жесткостей была учтена конструктивная арматура, установка которой повысила жесткость сечения.

Как видно на мозаике – балки и колонны постоянного сечения превратились в элементы переменной жесткости.

Где сечения больше нагружены (возникают трещины, жесткости элементарных площадок сечения падают в

соответствии с заданной диаграммой работы материала), там жесткость уменьшается значительней.

Выводы

В заключение еще раз следует отметить, что метод «Инженерная нелинейность» предназначен только для учета пониженной жесткости железобетонных конструкций в массовых инженерных расчетах и ни в коем случае не заменяет расчет с учетом физической нелинейности.

Метод «Инженерная нелинейность» реализован в программном комплексе ЛИРА-САПР. Таким образом, инженеры-проектировщики получили еще один инструмент, позволяющий учитывать в практических расчетах влияние пониженной жесткости железобетонных конструкций на НДС проектируемого сооружения. Такой подход позволяет выполнить более эффективное армирование железобетонных элементов и получить приближенные к реальным перемещениям конструкции. При этом существенно сокращается и время задания исходных данных для расчета, и время самого расчета, по отношению к шаговому физнелинейному расчету. Кроме того, «Инженерная нелинейность» доступна во всех конфигурациях программы, а шаговая физнелинейность только в комплектах PRO и FULL.

---

В ЛИРА-САПР 2018 разработан второй вариант инженерной нелинейности. В отличие от разработанной ранее, в "инженерной нелинейности 2" – реализованы новые подходы.

Концепции	Инженерная нелинейность 1 (прежняя версия)	Инженерная нелинейность 2
определяющее нагружение	можно включать произвольные нагружения	включаются реальные постоянно действующие нагружения
расчет на определяющее нагружение	итерационный	шаговый
задание арматуры	арматура подбирается в процессе итерационного расчета	арматура задается
расчет по традиционной схеме	расчет выполняется на все нагружения на основе секущих модулей деформации	расчет на временные нагрузки выполняется на основе касательного модуля деформации, соответствующего последнему шагу шагового расчета
учет физической нелинейности в монтаже	отсутствует	возможен
учет нелинейности в работе платформенных стыков	отсутствует	возможен

 

Список литературы

1. Бондаренко В. М. Инженерные методы нелинейной теории железобетона / В.М. Бондаренко – М.: Стройиздат, 1982. – 287 с.
2. Барабаш М. С. Компьютерное моделирование процессов жизненного цикла объектов строительства: Монография / Мария Сергеевна Барабаш. – К.: «Сталь», 2014. – 301 с
3. Городецкий А. С. К расчету физически нелинейных плоских рамных систем /А. С. Городецкий, В. С. Здоренко // Строительная механика и расчет сооружений. – 1969. – № 4. – С. 61-68.
4. Пикуль А. В. Определение жесткостных характеристик сечения железобетонного стержня с учетом нелинейных свойств материала / А.В. Пикуль, Д.А. Городецкий // Актуальные проблемы компьютерного моделирования конструкций и сооружений: тезисы докладов IV Международного симпозиума. – Челябинск.: Издательский центр ЮУрГУ, 2012. – С. 228.
5. Городецкий А. С. Учет нелинейной работы железобетонных конструкций в практических расчетах / А. С. Городецкий, М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2014. – Вып. 77. – С. 54–59.
6. Городецкий А. С. Компьютерное моделирование процесса нагружения железобетонных конструкций. Сборник научных трудов Луганского национального университета, серия «Технические науки» N49/52, - Л.: Из-во «ЛНАУ», 2004, с.3-10.

• инженерная нелинейность
• физическая нелинейность
• определяющее нагружение
• итерационный расчет
• определение жесткостных характеристик сечения
• пониженная жесткость железобетонных конструкций