Методы численного моделирования и расчета осадки здания

В программном комплексе «ЛИРА-САПР» есть возможность проводить расчет основания по различным моделям, в основе которых лежит трехмерная модель грунта, построенная на основе инженерно-геологических исследований.

Компьютерную модель основания можно осуществлять следующими методами:

1. Использование коэффициентов жесткости упругого основания С₁ и С₂.
   
2. Моделирование грунтового массива через объёмные КЭ:
   

• при использовании универсальных пространственных КЭ № 34, 36 для описания линейной деформации грунта;
• при использовании физически нелинейных объемных КЭ №271, 272, 273 (при задании различных вариантов условий прочности).

Наиболее распространенными видами аппроксимации работы неоднородного основания при статическом расчете конструкции являются одноузловые, пластинчатые или объемные конечные элементы. При использовании пластинчатых КЭ в ПК «ЛИРА-САПР» реализовано три метода определения коэффициентов постели: модель Пастернака, Винклера-Фусса и модифицированный расчет модели Пастернака.

Также, у пользователя есть возможность выбрать схему расчета осадки основания (линейно-деформированного полупространства или линейно-деформированного слоя).

Рассмотрим различные методы моделирования работы основания на примере расчётной схемы здания торгово-развлекательного центра.

В первой задаче, работа грунта моделировалась при помощи коэффициентов постели, которые были рассчитаны по модели Пастернака: С₁=25087.1кН/м³, С₂=4886.04кН/м.

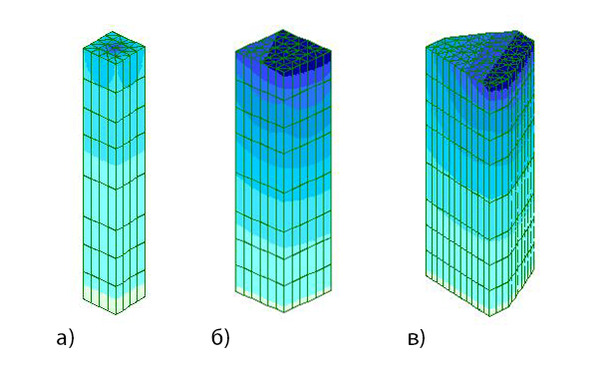
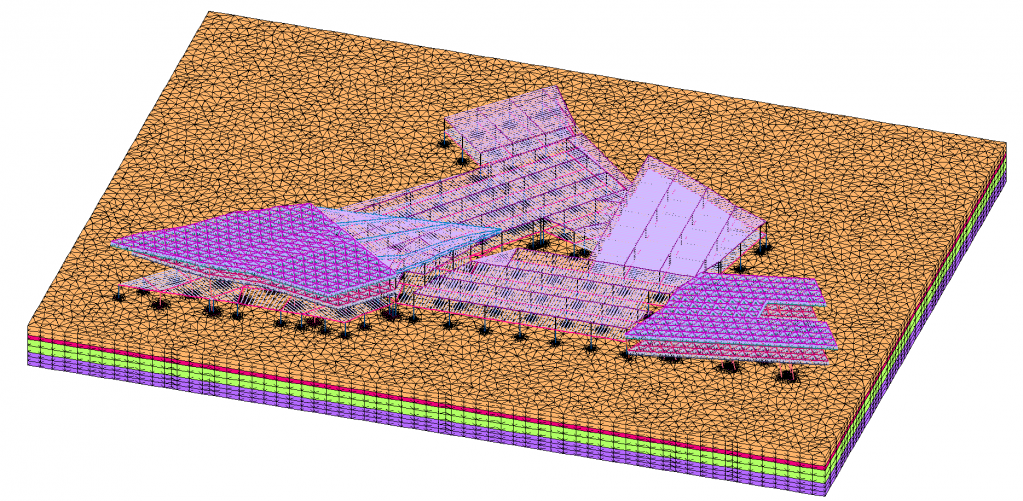
Во второй задаче, грунтовое основания было смоделировано при помощи объёмных КЭ. Данная задача состоит из двух частей: расчет основания в линейной постановке, и с учётом физической нелинейности поведения основания (при задании различных критериев прочности). Компьютерная модель здания и грунтового массива приведена на рисунке 2.

Если грунтовую среду моделировать как линейно деформированную, в ПК «ЛИРА-САПР» реализуется вычисление осадки основания от заданных нагрузок с использованием расчетной схемы в виде линейно деформированного полупространства (задача Буссинеска). В этой модели принимаются два предположения: первое – осадка  точки поверхности основания прямо пропорциональна величине загрузки  в этой точке, второе – осадка распространяется и за пределы площади загружения.

В отличие от предыдущего метода, модель линейно деформированного полупространства при совместном расчете сооружения с основанием позволяет определить кроме контактных напряжений, напряженно-деформированное состояние почвы всего основания.

При таком моделировании основы, с помощью объёмных конечных элементов, в качестве исходных данных вводятся только модуль общих деформаций E, коэффициент Пуассона n  и удельный вес каждого слоя. Толщина слоя задается при задании геометрии конечных элементов. При этом расчетная модель фактически сводится к сжатому слою конечной прочности.

В рассматриваемой задаче, конечным элементам были заданы следующие характеристики слоев грунтового массива: ИГЭ-1 (E= 28000 кН/м2, n = 0,3), ИГЭ-2 (E= 25000 кН/м2, n = 0,3), ИГЭ-3 (E= 13000 кН/м2, n = 0,3), ИГЭ-4 (E= 16000 кН/м2, n = 0,35).

Но деформацию грунта можно описать с помощью линейной модели среды лишь до определенного уровня усилий, за пределами которого линейная связь напряжений и деформаций нарушается.

Необратимые деформации грунта, как гетерогенной среды, возникают значительно раньше достижения предельного состояния, и они существенно превышают упругие деформации. Поэтому рассмотрим расчет осадки грунтового массива с учетом физически-нелинейной работы основания.

При решении этой задачи, для моделирования работы грунта, использовался КЭ273, который позволяет учитывать одностороннюю работу грунта с учетом сдвига. В данном случае, у пользователя есть возможность выбрать модель работы грунта (по Кулону-Мору, Друккеру-Прагеру или Боткину).

В рассматриваемом примере, для численного моделирования нелинейных свойств грунтового массива, конечным элементам №273 были заданы следующие характеристики:

– ИГЭ-1 (E= 28000 кН/м2, n = 0,3, R0= 17,4 кН/м3, ke= 1, C= 2 кН/м2, Rt= 2 кН/м2, Fi= 32˚, Ϭp= 300 кН/м2);

– ИГЭ-2 (E= 25000 кН/м2, n = 0,3, R0= 19,3 кН/м3, ke= 1, C= 1 кН/м2, Rt= 1 кН/м2, Fi= 30˚, Ϭp= 300 кН/м2);

– ИГЭ-3 (E= 13000 кН/м2, n = 0,3, R0= 19,1 кН/м3, ke= 1, C= 12 кН/м2, Rt= 5 кН/м2, Fi= 23˚, Ϭp= 280 кН/м2);

– ИГЭ-4 (E= 16000 кН/м2, n = 0,35, R0= 19,1 кН/м3, ke= 1, C= 25 кН/м2, Rt= 30 кН/м2, Fi= 22˚, Ϭp= 250 кН/м2);

где C – сцепление, Rt – предельное напряжение при растяжении, которое было определено из соотношения F_i – угол внутреннего трения, Ϭ_p – предельное напряжение сжатия.

Простой нелинейной моделью работы почвы является общеизвестная идеально упруго-пластическая модель с предельной поверхностью, что определяется критерием Кулона-Мора. Преимущество модели заключается в простоте назначения параметров, которые можно получить из отчета по инженерно-геологическим изысканиям. Для этой модели условие прочности выражается по формуле:

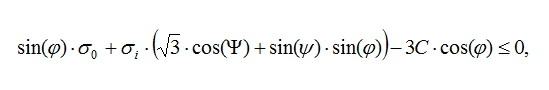
Однако, эта модель предусматривает одинаковое поведение материала на стадии первичного загружения и разгружения, что совсем не характерно для грунтов (в которых модуль загружения и разгружения отличается, как известно, в 5 ... 10 раз). Кроме того, недостатком данной модели является то, что в расчёте исключено главное промежуточное напряжение и его влияние на грунт, что не соответствует действительности, а наличие углов на поверхности текучести усложняет численное решение пространственных задач. Эти недостатки исключены при расчёте по критерию прочности Друккера-Прагера.

Модель Друккера-Прагера также реализует упругое идеально-пластическое поведение грунтов. А поверхность пластичности согласно модели Друккера-Прагера является правильным круговым конусом относительно гидростатической оси  в пространственной системе главных напряжений.

Условие прочности для модели Друкера-Прагера выражают по формуле:

    

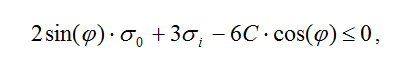
Также, в ПК «ЛИРА-САПР» реализовано условие прочности грунта Боткина. Согласно этому условию, в отличии от Кулона-Мора, предполагается, что на прочность почвы влияют все три главных напряжения, а предельное состояние наступает на октаэдрической плоскости (плоскость, является равнонаклонной ко всем главным направлениям напряжений).

Условие прочности для модели Боткина:

    

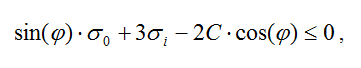
Сравнение и анализ результатов расчета было выполнено по ряду показателей: напряженное состояние наиболее загруженных колонн, величина максимального прогиба консольных стержневых элементов конструкции, кинематические характеристики – перемещение расчетных характерных точек здания по направлению «Z».

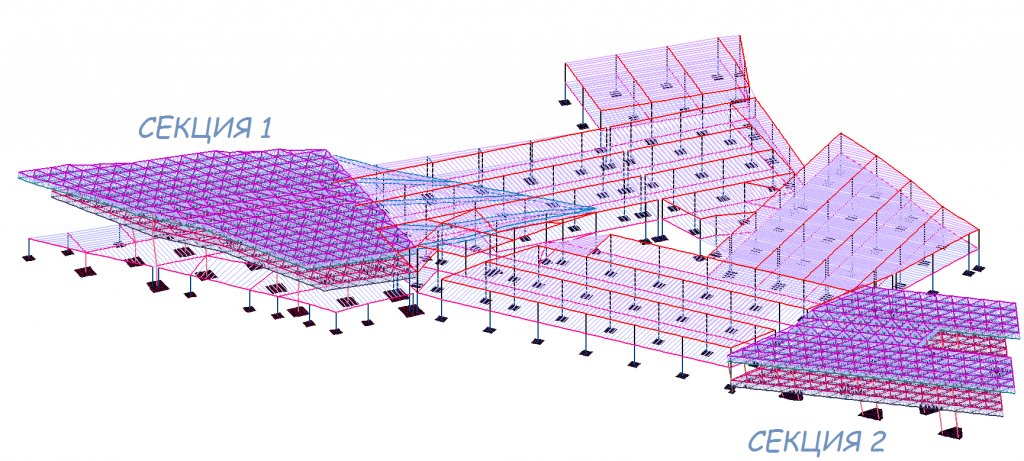
Численные значения максимальных прогибов консолей для каждого варианта моделирования грунтового основания приведены в таблице 1. Номера секций здания показаны на рисунке 3.

     

Таблица 1. Максимальные прогибы консольных частей здания, мм

Из таблицы видно, что полученные перемещения по результатам расчета при нелинейной постановке значительно выше, чем при использовании коэффициентов постели и КЭ34. Это объясняется тем, что КЭ273 лучше моделирует поведение основания, работа которого несомненно влияет на НДС элементов конструкции.

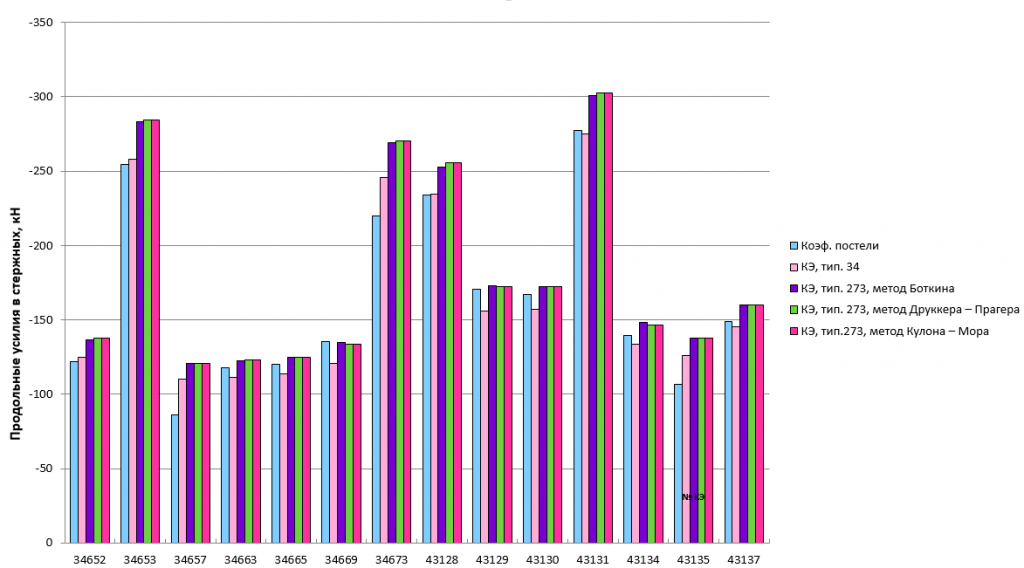
На рисунке 4 показано сравнение значений продольных усилий, что возникают в конечных элементах, которые моделируют работу самых загруженных колонн секции 2.

Результаты расчета в линейной постановке задачи и с учетом физической нелинейности основы характеризуются значительной степенью сходства. А погрешность в результатах при различных вариантах моделирования нелинейной работы основания менше 1%. Это указывает на то, что выбор метода описания нелинейной деформации элементов почти не играет роли при определении несущей способности и подборе сечений элементов конструкции.

На рисунке 6 приведена гистограмма по вертикальным перемещениям расчетных характерных точек фундаментных плит (ФП), которые обозначены кругами на рисунке 5. Изополя вертикальных перемещений рассматриваемых ФП показаны на рисунке 7.

ВЫВОДЫ

Выполненный анализ НДС  при различных вариантах моделирования грунтового массива показал, что максимальные значения осадки были получены при расчёте методом послойного суммирования. Разница между численным моделированием основания и при расчёте грунтового массива по методике линейно-деформированного полупространства с условным ограничением глубины сжимаемой толщи можно аргументировать несколькими факторами:

• в каждом элементарном слое вертикальные напряжения принимаются как среднее значение между дополнительным давлением на вершине и на подошве каждого слоя. Такая апроксимация эпюр напряжений не даёт достаточной возможности описать работу дисперсной среды;
  
• отсутсвие сил взаимодействия между элементарными слоями;
  
• в методе послойного суммирования не учитывается нелинейное изменение величины модуля деформаций для каждого элементарного слоя.
  

Погрешность при расчётах осадки здания при различных методах моделирования нелинейной работы грунта составляет в основном меньше 1%. При учёте пластической работы основания метод Кулона-Мора показал наименьшие значения осадки. Это можно обьяснить тем, что данная модель не учитывает влияния главного промежуточного напряжения. Этот фактор был учтён в методе Боткина, где принимается во внимание связь  интенсивности касательных напряжений и среднего давления. Именно при использовании этого метода были получены максимальное значения осадки конструкции при компьютерном моделировании системы.

• численное моделирование
• напряженно-деформированное состояние
• осадка
• метод послойного суммирования
• физическая нелинейность